Part Of: Algebra sequence
Content Summary: 1300 words, 13 min read.

Linear algebra is the math of vectors and matrices. Let me attempt to explain it as succinctly as possible.

Vector Operations

If n is a positive integer and ℝ is the set of real numbers, then ℝⁿ is the set of all n-tuples of real numbers.  A vector v ∈ ℝⁿ is one such n-tuple. For example,

The six vector operations are: addition, subtraction, scaling, cross product, dot product, norm (vector length). For vectors u and v, these are defined as follows:

The dot product and the cross product norm are related to the angle between two vectors. Specifically,

Finally, note the the cross product is not commutative: u x v != v x u.

Matrix Operations

A matrix A ∈ ℝ^{m x n} is a rectangular array of real numbers with m rows and n columns. For example,

Important matrix operations are addition, subtraction, product, transpose, and determinant:

Of the above operations, matrix product is especially significant. This operation is only possible when A has the same number of columns as B has rows.

Matrix as Morphism

Importantly, matrices with one row or one column can interpreted as vectors. Matrix multiplication with a vector can be interpreted in two ways. The row picture interprets the output as a dot product, the column picture interprets the output as a linear combination.

Let’s take A to be a 2 by 2 matrix with row-vectors (2, -1) and (-1,2), and let b = (0,3). When we solve for x, we find there are two ways to do so:

In the above example, we set b = (0,3). But this linear combination could generate any vector b. In general, linear combinations can generate the entirety of a space (in this case, a two-dimensional plane). 

In both views, we say A transform x → b. If vectors are groups of data, matrices are functions that operate on vectors. Specifically, multiplication by a matrix A ∈ ℝ^{m x n} we will call a linear transformation, that converts an n-tuple into a m-tuple T_A : ℝⁿ → ℝ^m.

The symmetry between functions and linear transformations runs deep. When we explore category theory, we will discover the structure underpinning this relationship. But in the meantime, consider the following equivalences:

Especially important to matrix functions is the notion of inverse matrix. Just as f^-1(x) = ln(x) undoes the effects of f(x) = e^x, inverse matrix A^-1 undoes the effects of A. The cumulative effect of applying A^-1 after A is the identity matrix A^-1A = 1. The identity matrix is analogous to multiplying by one, or adding zero: it is algebraically inert.

Only square matrices can be invertible, because reversal is commutative AA^-1 = A^-1A = 1. But not all square matrices have inverses. The determinant of a matrix checks for invertibility. Det(A) != 0 iff A is invertible.

Matrix inversion is vitally important to solving systems of linear equations.

• AX = B → multiply both sides by A^-1 on the right → X = A^-1B
• XA = B → multiply both sides by A^-1 on the right → X = BA^-1
• ABXC = E → put C^-1 on the right and B^-1A^-1 on the left → X = B^-1A^-1EC^-1

Elimination As Inverse Solver

To solve Ax = b, we must find inverse matrix A^-1. This can be done via Gauss-Jordan Elimination. This method affords three row operations:

1. Linear Combination: R_i += kR_j
2. Scaling: R_i *= k
3. Row Swap: R_i ⇆ R_j

After creating a matrix of the form Ax = b, we can solve for x by creating an augmented matrix of the form [ A | b ], and converting the left-hand side into the identity matrix:

To solve for x algebraically, Ax = b → A^-1Ax = A^-1b → 𝟙x = A^-1b. So Gauss-Jordan facilitates the discovery of inverse matrix A^-1. We can show this computation explicitly, by setting an augmented matrix of form [ A | 1 ]

Row operations are functions that act on vectors. So are matrices. Thus, it isn’t very surprising that our three row operations each correspond to an elementary matrix. The elementary matrix is similar to the identity matrix; in the below picture, only the shaded region diverges. 

We now see that the row operations of Gauss Jordan elimination are a kind of factoring: we are finding the elementary matrices underlying A^-1:

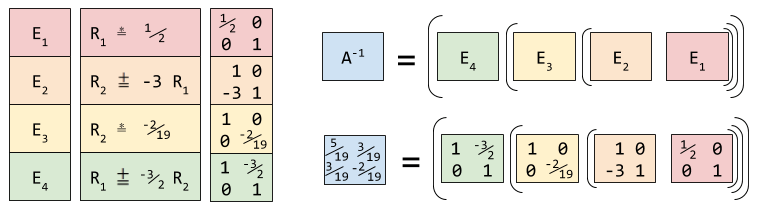
Thus E₄E₃E₂E₁ = A^-1 and Ax = b → (E₄E₃E₂E₁)Ax = (E₄E₃E₂E₁)b → x = A^-1b

Fundamental Vector Spaces

A vector space consists of a set of vectors and all linear combinations of these vectors. The set of all linear combinations is called the span. For example, the vector space S = span{ v₁, v₂ } consists of all vectors of the form v = ɑv₁ + βv₂, where ɑ and β are real numbers.

Vector spaces can be characterized by a basis: the original set of vectors whose linear combination creates the vector space. The vectors of any basis must be linearly independent, or orthogonal. You can check whether two vectors or orthogonal by confirming their dot product u · v = 0. The dimension of a vector space is the cardinality of the basis (number of orthogonal vectors).

Recall that matrices are functions that project vectors from ℝⁿ to ℝ^m. This corresponds to projecting from row space to column space, as follows:

We will unpack the full implications of this graphic another time. For now, it suffices to understand that discovering the bases of these subspaces is a useful exercise.

For example, if we show that a matrix has an non-empty kernel, this in itself is proof of non-invertibility. Why? Because if T_A sends a vector to the zero vector, there is no T_A^-1 that can undo this operation.

We can say more. For an n x n matrix A, the following statements are equivalent:

1. A is invertible
2. The determinant of A is nonzero.
3. The RREF of A is the n x n identity matrix
4. The rank of the matrix is n
5. The row space of A is ℝⁿ
6. The column space of A is ℝⁿ
7. A doesn’t have a null space (only the zero vector N(A) = {0} )

Elimination as Basis Identifier

We have seen elimination discover (and factorize) the matrix inverse. But what happens when an inverse does not exist? Well, elimination has a natural, unique stopping point:

Matrices in reduced row echelon form (RREF) have the following properties:

1. Rows with all zeroes are moved to the bottom.
2. The first nonzero number from the left (pivot) is to the right of the pivot above it.
3. Every pivot equals 1 and is the only nonzero entry in its column

Gauss-Jordan Elimination can replace every matrix with an equivalent one in rref form. Note that we have seen several examples of elimination creates the identity matrix 1  when A is invertible. This is only possible because 1 fits the rref criteria.

Once a matrix is in rref form, it becomes trivial to discover the basis for its three fundamental spaces:

• R(A) basis: all row vectors that are non-zero
• C(A) basis: all column vectors that contain pivot.
• N(A) basis: the solution to Ax = 0

We see that rank(A) + nullity(A) = 3 + 1 = 4, which indeed is the number of columns. Also, the column space of A equals the row space of A^T. This is not an accident, since transpose simply swaps rows with columns.

Takeaways

• Vectors are groups of numbers; matrices are functions that act on vectors.
• We can solve linear equations by conducting Gauss-Jordan elimination.
• Gauss-Jordan elimination-based solution rely on searching for inverse matrix A^-1
• The domain of matrices is its row vectors, its codomain is its column vectors.
• Even if a matrix is not invertible, elimination can find its most reduced form (RREF).
• RREF matrices can be used to derive fundamental subspaces.

Until next time.

Related Works

• Linear Algebra in Four Pages
• SageMath can be used to check my work