Followup To: Logic Structure: Connectives in IPL
Part Of: Logic sequence
Content Summary: 300 words, 3 min read

Motivations

Last time, we looked at Intuitionistic Propositional Logic (IPL). In IPL, there are five connectives, and hence five introduction-elimination pairs:

What if you had to design a new logic from scratch? Suppose we were to invent five new connective symbols. Would you start by defining their introduction rule, and use these to infer elimination? Or would you instead define elimination first?

This choice reflects different ways to interpret the semantics of logic:

• The verificationist starts with introduction first. For them, the meaning of a connective is in their constructor (introduction rules).
• The pragmatist starts with elimination first. For them, the meaning of a proposition is how you use it.

But if introduction and elimination rules agree, then a logical system has harmony.

How do we evaluate harmony in practice? Harmony is defined as two propositions:

• Local soundness: if I introduce and then eliminate a connective, do I gain information? If so, the elimination rule is too weak.
• Local completeness: if I eliminate then re-introduce connective, do I lose information? If so, the elimination rule is too strong.

Demonstrating Harmony in IPL

We can show that conjunction rules exhibit harmony.

Note that we have only shown soundness for left-elimination. But demonstrating soundness for right-elimination is highly analogous.

Implication rules also exhibit harmony.

So does disjunction.

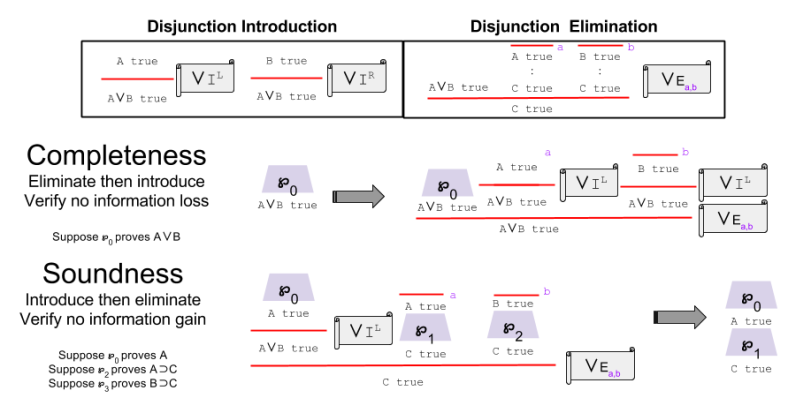
It is trivial to demonstrate the harmony of truth and falsity. Thus, we can say that IPL, as a formal system, has harmony.

Takeaways

In this article, we have discussed harmony, which helps us evaluate how useful a given formal system is. This notion may seem straightforward in IPL; however, it will prove useful in designing new logics, such as linear logic.

Another more subtle point to consider is that the soundness demonstration also seems to reflect a logic of simplification. This point will return when we discuss the Curry-Howard-Lambek correspondence, and the deep symmetries between logic and computation.

Until next time.