Author kevinbinz

An Introduction To Natural Selection

kevinbinz Leave a comment

Part Of: Demystifying Life sequence
Followup To: Population Genetics
Content Summary: 1400 words, 14 min read

How Natural Selection Works

Consider the following process:

  1. Organisms pass along traits to their offspring.
  2. Organisms vary. These random but small variations trickle through the generations.
  3. Occasionally, the offspring of some individual will vary in a way that gives them an advantage.
  4. On average, such individuals will survive and reproduce more successfully.

This is how favorable variations come to accumulate in populations.

Let’s plug in a concrete example. Consider a population of grizzly bears that has recently migrated to the Arctic.

  1. Occasionally, the offspring of some grizzly bear will have a fur color mutation that renders their fur white.
  2. This descendent will on average survive and reproduce more successfully.

Over time, we would expect increasing numbers of such bears to possess white fur.

Biological Fitness Is Height

The above process is straightforward enough, but it lacks a rigorous mathematical basis. In the 1940s, the Modern Evolutionary Synthesis enriched natural selection by connecting it to population genetics, and its metaphor of Gene-Space. Recall what we mean by such a landscape:

  • A Genotype Is A Location.
  • Organisms Are Unmoving Points
  • Birth Is Point Creation, Death Is Point Erasure
  • Genome Differences Are Distances

Onto this topography, we identified the following features:

  • A Species Is A Cluster Of Points
  • Species Are Vehicles
  • Genetic Drift is Random Travel.

In order to understand how natural selection enriches this metaphor, we must define “advantage”. Let biological fitness refer to how how many fertile offspring an individual organism leaves behind. An elephant with eight grandchildren is more fit than her neighbor with two grandchildren.

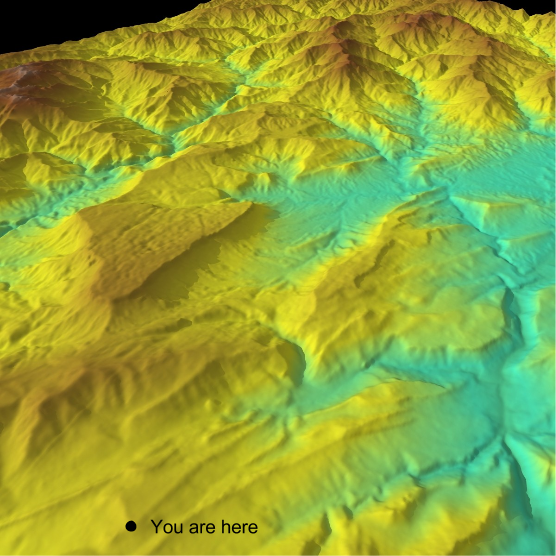
Every organism achieves one particular level of biological fitness. Fitness denotes how well-suited an organism is to its environment. Being a measure of organism-environment harmony, we can view fitness as defined for every genotype. Since we can define some number for every point in gene-space, we have license to introduce the following identification:

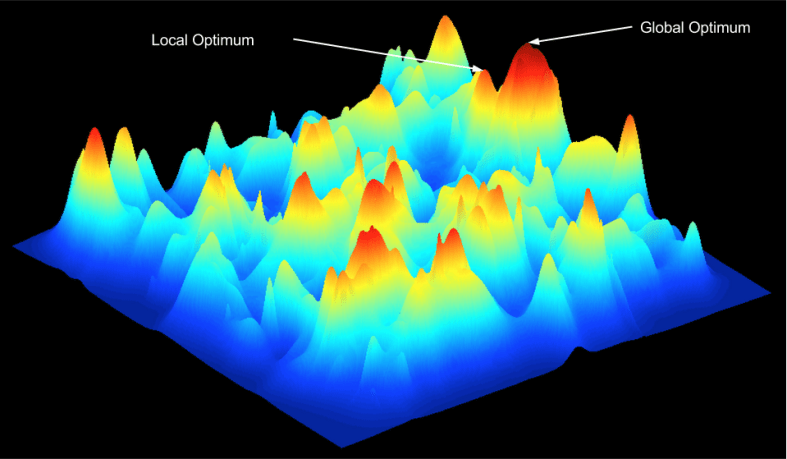
  • Biological Fitness Is Height

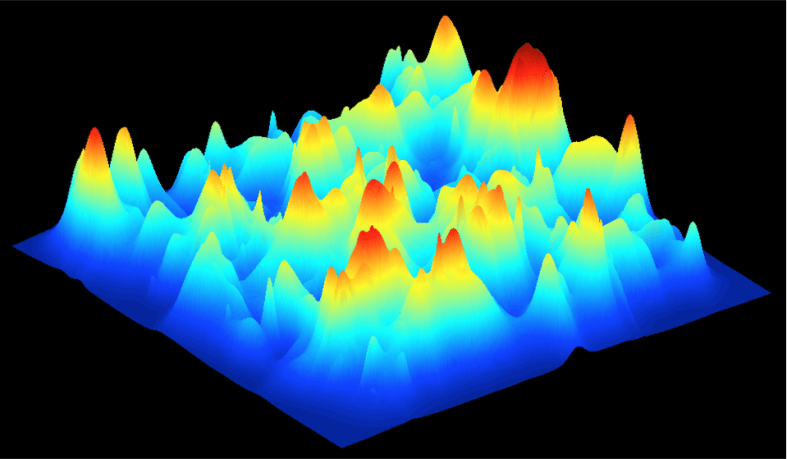
Here is one possible fitness landscape (image credit Bjørn Østman).

Natural Selection- Fitness Landscape (1)

We can imagine millions of alien worlds, each with its own fitness landscape. What is the contours of Earth’s?

Let me gesture at three facts of our fitness landscape, to be elaborated next time:

  • The total volume of fitness is constrained by the sun. This is hinted at by the ecological notion of carrying capacity.
  • Fitness volume can be forcibly taken from one area of the landscape to another. This is the meaning of predation.
  • Since most mutations are harmless, the landscape is flat in most directions. Most non-neutral mutations are negative, but some are positive (example).

Natural Selection As Mountain Climbing

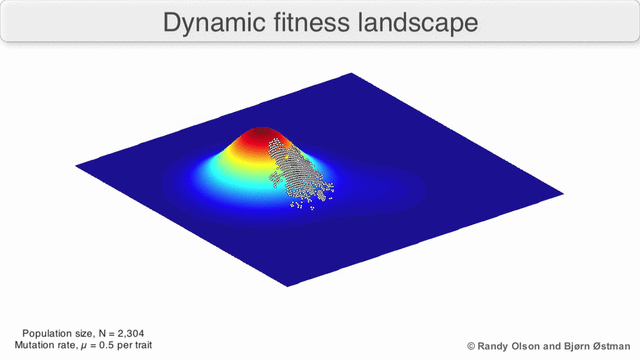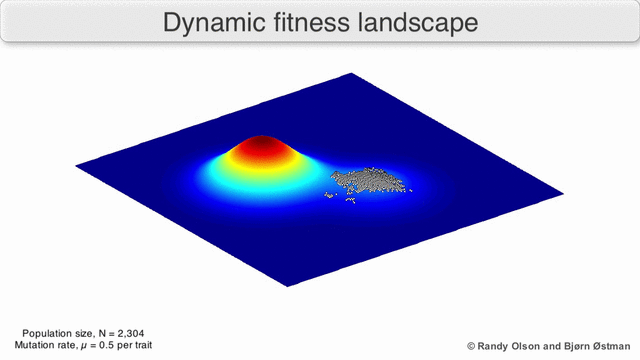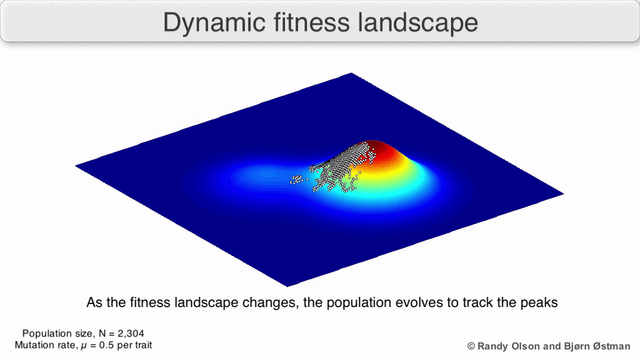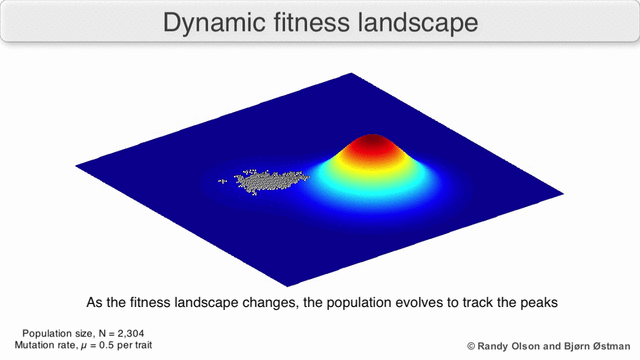
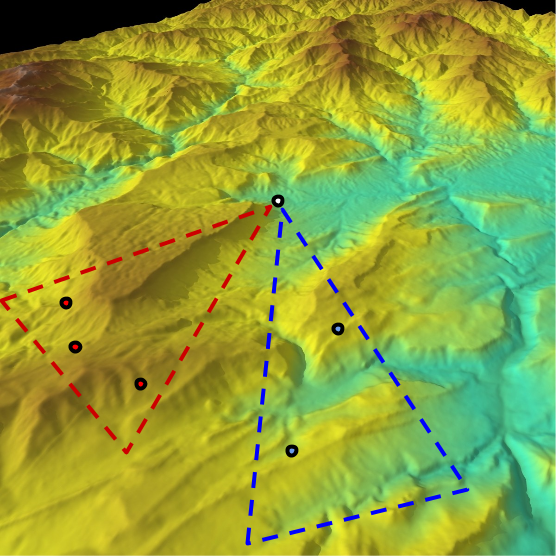
A species is a cluster of points. Biological fitness is height. What happens when a species resides on a slope?

The organisms uphill will produce comparatively more copies of themselves than those downhill. Child points that would have been evenly distributed now move preferentially uphill. Child points continue appearing more frequently uphill. This is locomotion: a slithering, amoeba-like process of genotype improvement.

NaturalSelection_Illustration

We have thus arrived at a new identification:

  • Natural Selection Is Uphill Locomotion

As you can see, natural selection explains how species gradually become better suited to their environment. It is a non-random process: genetic movement is in a single direction.

Consider: ancestral species of the camel family originated in the American Southwest millions of years ago, where they evolved a number of adaptations to wind-blown deserts and other unfavorable environments, including a  long neck and long legs. Numerous other special designs emerged in the course of time: double rows of protective eyelashes, hairy ear openings, the ability to close the nostrils, a keen sense of sight and smell, humps for storing fat, a protective coat of long and coarse hair (different from the soft undercoat known as “camel hair”), and remarkable abilities to take in water (up to 100 liters at a time) and do without it (up to 17 days).

Moles, on the other hand, evolved for burrowing in the earth in search of earthworms and other food sources inaccessible to most animals. A number of specialized adaptations evolved, but often in directions opposite to those of the camel: round bodies, short legs, a flat pointed head, broad claws on the forefeet for digging. In addition, most moles are blind and hard of hearing.

The mechanism behind these adaptations is selection, because each results in an increase in fitness, with one exception. Loss of sight and hearing in moles is not an example of natural selection, but of genetic drift: blindness wouldn’t confer any advantages underground, but arguably neither would eyesight.

Microbiologists in my audience might recognize a strong analogy with bacterial locomotion. Most bacteria have two modes of movement: directed movement (chemotaxis) when its chemical sensors detect food, and a random walk when no such signal is present. This corresponds with natural selection and genetic drift, respectively.

Consequences Of Optimization Algorithms

Computer scientists in my audience might note a strong analogy to gradient descent, a kind of algorithm. In fact, there is a precise sense in which natural selection is an optimization algorithm. In fact, computer scientists have used this insight to design powerful evolutionary algorithms that spawn not one program, but thousands of programs, rewarding those with a comparative advantage. Evolutionary algorithms have proven an extremely fertile discipline in problem spaces with high dimensionality. Consider, for example, recent advances in evolvable hardware:

As predicted, the principle of natural selection could successfully produce specialized circuits using a fraction of the resources a human would have required. And no one had the foggiest notion how it worked. Dr. Thompson peered inside his perfect offspring to gain insight into its methods, but what he found inside was baffling. The plucky chip was utilizing only thirty-seven of its one hundred logic gates, and most of them were arranged in a curious collection of feedback loops. Five individual logic cells were functionally disconnected from the rest— with no pathways that would allow them to influence the output— yet when the researcher disabled any one of them the chip lost its ability to discriminate the tones…

It seems that evolution had not merely selected the best code for the task, it had also advocated those programs which took advantage of the electromagnetic quirks of that specific microchip environment. The five separate logic cells were clearly crucial to the chip’s operation, but they were interacting with the main circuitry through some unorthodox method— most likely via the subtle magnetic fields that are created when electrons flow through circuitry, an effect known as magnetic flux. There was also evidence that the circuit was not relying solely on the transistors’ absolute ON and OFF positions like a typical chip; it was capitalizing upon analogue shades of gray along with the digital black and white.

In gradient descent, there is a distinction between global optima and local optima. Despite the existence of an objectively superior solution, the algorithm cannot get there due to its fixation with local ascent.

Natural Selection- Local vs. Global Optima

This distinction also features strongly in nature. Consider again our example of camels and moles:

Given such a stunning variety of specialized differences between the camel and the mole, it is curious that the structure of their necks remains basically the same. Surely the camel could do with more vertebrae and flex in foraging through the coarse and thorny plants that compose its standard fare, whereas moles could just as surely do with fewer vertebrae and less flex. What is almost as sure, however, is that there is substantial cost in restructuring the neck’s nerve network to conform to a greater or fewer number of vertebrae, particularly in rerouting spinal nerves which innervate different aspects of the body.

Here we see natural selection as a “tinkerer”; unable to completely throw away old solutions, but instead perpetually laboring to improve its current designs.

Takeaways

  • In the landscape of all possible genomes, we can encode comparative advantages as differences in height.
  • Well-adapted organisms are better at replicating their genes (in other words, none of your ancestors were childless).
  • Viewed in the lens of population genetics, natural selection becomes a kind of uphill locomotion.
  • When view computationally, natural selection reveals itself to be an optimization algorithm.
  • Natural solution can outmatch human intelligence, but it is also a “tinkerer”; unable to start from scratch.

[Sequence] Biology

kevinbinz Leave a comment
Population Genetics- Ring Species (2)

Life sequence

Evolution sequence

Life History sequence

Brain Evolution sequence

Earth Science sequence

Older Posts

An Introduction To Population Genetics

kevinbinz Leave a comment

Part Of: Demystifying Life sequence
Content Summary: 1200 words, 12 min read

Central Thesis Of Molecular Biology

In every cell of your body, there exist molecules called deoxyribonucleic acid. Such cells come in four flavors and (due to their atomic shape) tend to pair up and create long strings. These strings become very long, over two inches when held end-to-end (but of course, they fold up dramatically so each can comfortably inhabit a single cell). Since your cells have about 46 inches worth (six billion molecules), each cell contains twenty-three unique strings. They look like this:

Natural Selection- Chromosomes

Let us refer to these strings as chromosomes, and to all of them collectively as the human genome. Finally, since typing “deoxyribonucleic acid” is fairly onerous, we will use the acronym DNA.

In 1956, Francis Crick presented his Central Thesis Of Molecular Biology, which describes how the causal chain DNA → RNA → amino acids → protein ultimately motivates every trait of every living organism.  A gene is a sequence of DNA that encodes a protein. A genotype (some animal’s unique DNA) explains phenotype (that animal’s unique traits).  Genotype-phenotype maps (GP-maps) turn out to be very important in what follows.

Duplication vs. Mutation

Every time a cell duplicates itself (mitosis), its DNA is copied into the new cell. If every cell contains exactly the same code, how can they be different? The basic explanation of cellular differentiation involves feedback loops in the genetic causal chain (collectively named the Gene Regulatory Network). When a lung cell is duplicated, for example, it inherits not just the entire genome, but also proteins for activating lung genes and deactivating other code.

Germ cells are created by a different process entirely. Instead of genome duplication (mitosis), germ cells inherit what is essentially half a genome, in a process known as meiosis. Here’s how these two processes work:

Natural Selection- Mitosis vs. Meiosis

Recall that deoxyribonucleic acid is a collection of atoms. Replicating such a fragile object is imperfect. There are many kinds of ways the process can go wrong; for example:

  1. Replacement Mutation (e.g., AGTC → AATC)
  2. Duplication Mutation (e.g., AGTC → AGGTC)
  3. Insertion Mutation (e.g., AGTC → AGATC)

How many mutations do you have? While you can always get your DNA sequenced to find out, the answer for most people is about sixty.

The Landscape Of Gene-Space

Consider all animals whose genome is three molecules long. How many genetically unique kinds of these animals are there?  Recall there are four kinds of DNA: cytosine (C), guanine (G), adenine (A), or thymine (T). We can use the following formula:

|Permutations| = |Possibilities|^{|Slots|}

Here we have 3^4 = 81 possible genotypes in this particular gene-space. To visualize this, imagine a 4-sided Rubik’s Cube: each dimension is a slot, each cube a particular genotype in the space.

But humans have approximately three billion base pairs; the size of a realistic gene-space is almost incomprehensibly large (4^3,000,000,000), far exceeding the number of atoms in the universe. Reasoning about 3D cubes is easy, reasoning about 3,000,000,000-D hypercubes is a bit harder. So we employ dimension reduction to aid comprehension. If you laid all 4^3,000,000,000 numbers out on a two dimensional matrix, each cell would be so tiny that the surface would appear continuous. We have arrived at our first metaphor identification:

  • A Genotype Is A Location

We can summarize our discussion of mitosis, meiosis, and mutation as follows:

  • An Organism Is A Stationary Point
  • Birth Is Point Creation, Death Is Point Erasure.

Finally, let us explore the concept of genetic distance. From our toy gene-space, let me take seven nodes and draw lines indicating valid replacement mutations between them.

Population Genetics- Visualizing Genetic Distance

The key observation is that distances vary. Many nodes are connected via one mutation, but the minimum distance from top (ATG) to bottom (CCC) is three mutations. In other words:

  • Varying Genome Differences Are Varying Distances

Our gene-space landscape, then, looks something like this:

Population Genetics- Gene Landscape (1)

Species Are Clusters

What is a species? After all, there is no encoding of the word “jaguar” in the jaguar genome. Rather, members of a species share more genetic similarities to one another than other organisms. In terms of our metaphor:

  • A Species Is A Cluster Of Points

In the above landscape, we might have two species. But there are many ways to cluster data. Consider these competing definitions:

Population Genetics- Species Granularity (1)

Which clustering approach is correct? It depends on the scale of our axes:

  • If we chose Granular but are too “zoomed in”, we have accidentally defined four new species of Shih Tzu.
  • If we chose Course but are too “zoomed out”, we have accidentally defined Mammal as its own species.

The point is that scale matters, and we should define species on a scale that makes good biological sense. The most popular scale is that defined by successful interbreeding (i.e., produce fertile offspring). For greater distances (large genetic dissimilarity), such interbreeding is impossible. We therefore constrain the size of our specie clusters by maximum interbreeding distance.

The approach just outlined is the one in use today. However, any man-made criteria for categorizing reality has its stretch points. For example, consider ring species.

Population Genetics- Ring Species (2)

Consider the Larus gulls’ populations in the above image. These gulls habitats form a ring around the North Pole, not normally crossed by individual gulls. The European herring gull {6} can hybridize with the American herring gull {5}, which can hybridize with the East Siberian herring gull {4} which can hybridize with Heuglin’s gull {3}, which can hybridize with the Siberian lesser black-backed gull {2}, which can hybridize with the lesser black-backed gulls {1}. However, the lesser black-backed gulls {1} and herring gulls {6} are sufficiently different that they do not normally hybridize.

Genetic Drift Is Random Travel

Landscapes without movement aren’t very interesting. With our brand-new concept as Species As Clusters, let’s see if we can make sense of travel.

Consider the phenomenon of population bottleneck. Many factors may contribute to population reduction (e.g., novel predators). Often, the survivors are just lucky. Descendants of the survivors tend to be more similar to them than the average genome of the original species. By this process, bottlenecks induces change in the species as a whole:
Population Genetics- Genetic Drift (1)

Why wouldn’t such movement cancel itself out in the long run? The reason why resides in the size of gene-space. For our genome is length two, mutations cancelling each other out would be a fairly common occurence. Would cancelling out increase or decrease on a genome of length 1,000? Surely less. How much less (a forteriori!)  the case for genomes with three billion molecules. By the extreme dimensionality of gene-space, then, we are witness to non-cancellative genetic movement!

  • Genetic Drift Is (Random) Travel.

Importantly, it is not the individuals that travel (modify their genomes), but the species as a whole.

  • Species Are Vehicles.

Viewing the species itself as actor, rather than the individual, is an important paradigm shift of population genetics.

Takeaways

In this post, I introduced the following metaphor:

  • A Genotype Is A Location.
  • Organisms Are Unmoving Points
  • Birth Is Point Creation, Death Is Point Erasure
  • Genome Differences Are Distances

We then strengthened our metaphor with the following considerations:

  • A Species Is A Cluster Of Points
  • Species Are Vehicles
  • Genetic Drift is (Random) Travel.

We are left with the image of specie vehicles clumsily moving around gene-space. But genetic drift is not the only mechanism by which species navigate gene-space. In our next post, we explore a more sophisticated property of living things.

[Sequence] Desmystifying Ethics

kevinbinz Leave a comment

Philosophy of Morality

Evolution of Morality

Moral Cognition

Older Posts

Applied Ethics

Epistemic Topography

kevinbinz 1 Comment

Related To: [Metaphor Is Narrative]
Content Summary: 1600 words, 16 min read.

Ambassadors Of Good Taste

I concluded my discussion of metaphor with three takeaways:

  • Metaphor relocates inference: we reason about abstract concepts using sensorimotor processes.
  • Metaphor imbues communication with affective flair or style.
  • Weaving metaphors together is narrative paint.

Let me build on such theses with the following aphorisms:

  • Metaphors which generate accurate empirical predictions are apt. Not all metaphors have this quality.
  • Metaphorical aptitude is a continuous scale, with complex empirical predictions generating higher scores.
  • Improving metaphorical aptitude is a design process.
  • Scientists who immerse their empirical results into this process are, in my language, ambassadors of good taste.

This post strives to develop a metaphor with high aptitude. You are witness to what I mean by “design process”.

Anatomy Of A Metaphor

Concept-space is useful because it sheds light on the nature of learning. The central identifications are:

  • A World Model Is A Location.
  • The Reasoner Is A Vehicle
  • Inference Is Travel

Our unconscious selves already use this metaphor frequently (c.f. phrases like “I’m way ahead of you.”) We aren’t inventing something so much as refining it.

To these three pillars, another identification can be successfully bolted on:

  • Predictive Accuracy Is Height

As we will see, pursuing knowledge really is like climbing a mountain.

Epistemic Topology- Your Location

Need For Cognition is Frequency Of Travel

Let’s talk about need for cognition: that personality trait that disposes some people towards critical thinking.

Those who know me, know how deeply I am driven to interrogate reality. Why am I like this? My answer:

I pursue deep questions because I tell myself I am curious → I tell myself I am curious because I pursue deep questions.

Such identity bootstrapping appears in other contexts as well. For example:

I am generous with my time because I tell myself I am selfless → I tell myself I am selfless because I am generous with my time.

Curiosity is an itch, active curiosity is scratching it. In terms of our metaphor:

  • If inference is travel, actively curious people are those who travel more frequently.

Intelligence is Vehicular Speed

Where does intelligence – that mental ability linked to abstraction – fit? Consider the following:

  • Although our society tends to lionize IQ as a personal trait, intelligence is mostly (50-80%) genetic. High-IQ parents tend to have high-IQ children, and vice versa.
  • What’s more, intelligence is highly predictive of success in life. It is so important for intellectual pursuits that eminent scientists in some fields have average IQs around 150 to 160. Since IQ this high only appears in 1/10,000 people or so, it beggars coincidence to believe this represents anything but a very strong filter for IQ.
  • In other words, Nature is not going to win any awards for egalitarianism any time soon.

We interpret intelligence as follows:

  • If the reasoner is a vehicle, intelligence is the speed of her vehicle.

If this topic conjures up existential angst (“I’ll never study again!” :P) check out this post. Speaking from my own life, my need for cognition is comparatively stronger than my intelligence quotient. In the tortoise-vs-hare race, I am the tortoise. 

On Education And Directional Calibration

One might reasonably complain that learning is not a solitary activity – our metaphor is too individualistic.

Let’s fix it. Consider the classroom. A teacher typically knows more than her students; in our metaphorical space, she is elevated above them. But the incomprehensible size of concept-space entails three uncomfortable facts:

  1. Every student resides in a different location.
  2. Knowing the precise location is computationally infeasible (even one’s own location).
  3. Without such knowledge, discovering to that student’s optimal path up the mountain is also infeasible.

Fortunately, location approximations are possible. Imagine a calculus professor with five students. Three students are stuck on the mathematics of the chain rule, the other two don’t grok infinitesimals. We might imagine the first group in the SW direction and the second are S-SE:

Epistemic Topology- Relative Location Groups (1)

Without knowing anyone’s precise location, the professor (white dot) can provide the red group with worked examples of the chain rule (direct to the NE) and the blue group with stories to motivate the need for infinitesimals (direct to N-NW). While such directional calibration is imprecise, it nevertheless gets them closer to the professors’ knowledge (amplifying their predictive power).

Epistemic Topology- Directional Calibration (2)Notice how each student travels along different speeds (intelligence) and frequencies (work ethic).

On Inferential Distance

If the process of building World Models is a journey, the notion of inferential distance becomes relevant.

Imagine reading two essays and then being quizzed for comprehension. Both have the same word count; one is written by a theoretical physicist, the other by a journalist. The physicist’s writings would probably take longer to understand. But why is this so?

Surely there is a greater inferential distance between us and the theoretical physicist. Is it so surprising that traveling greater distances consume more time?

This intuition sheds light on a common communication barrier, which Steven Pinker frames well:

Why is so much writing so bad?

The most popular explanation is that opaque prose is a deliberate choice. Bureaucrats insist on gibberish to cover their anatomy. Plaid-clad tech writers get their revenge on the jocks who kicked sand in their faces and the girls who turned them down for dates. Pseudo-intellectuals spout obscure verbiage to hide the fact that they have nothing to say, hoping to bamboozle their audiences with highfalutin gobbledygook.

But the bamboozlement theory makes it too easy to demonize other people while letting ourselves off the hook. In explaining any human shortcoming, the first tool I reach for is Hanlon’s Razor: Never attribute to malice that which is adequately explained by stupidity. The kind of stupidity I have in mind has nothing to do with ignorance or low IQ; in fact, it’s often the brightest and best informed who suffer the most from it.

The curse of knowledge is the single best explanation of why good people write bad prose. It simply doesn’t occur to the writer that her readers don’t know what she knows—that they haven’t mastered the argot of her guild, can’t divine the missing steps that seem too obvious to mention, have no way to visualize a scene that to her is as clear as day.

The curse of knowledge expects short inferential distances. Why does this bias (not another) live in our brains?

As we have seen, estimating location is expensive.  So the brain takes a shortcut: it uses a location it already knows about (its own) and employs differences between the Self and the Other to estimate distance. Call this self-anchoring. But the brain isn’t aware of all differences, only those it observes. Hence the process of “pushing out” one’s estimation of Other Locations typically doesn’t go far enough… the birthplace of the curse.

On Epistemic Frontiers, Fences, and Cliffs

It is tempting to view cognition as transcendent. Cognition transcendence plays a key role in debates over free will debates, for example. But I will argue that barriers to inference are possible. Not only that, but they come in three flavors.

Intelligence is speed, but is there a speed limit? There exist physical reasons to answer “yes”; instantaneous learning is as absurd as physical teleportation.  Just as a light cone constrains how physical event spreads through the universe, we might appeal to a cognition cone. Our first barrier to inference, then, is running out of gasoline. Death represents an epistemic frontier, with intellectually gifted people enjoying wider frontiers. Arguably, the frontier of anterograde amnesiacs is much shorter, defined by the frequency at which their memories “reset”.

If most education eases inference, we might imagine other social devices that retard that very same movement. Examples abound of such malicious, man-made epistemic fences. While conspiracy theories typically rely on naive models of incentive structures, other forms of information concealment plague the world. Finally, people steeped in cognitive biases (e.g., cult members within a happy death spiral) cannot navigate concept-space normally.

Epistemic frontiers need not concern us overly much (e.g., educational inefficiencies inhibit progress more than short lifespans).  Epistemic fences are more malicious, but we can still dream of moving away from tribalism.  What about permanent barriers? Might naturally-occurring epistemic cliffs inhabit our intellectual landscape? Yes. Some of the more well-known cliffs include Godel’s Incompleteness Theorems, and the Heisenberg Uncertainty Principle.

We have seen three types of inferential stumbling blocks: finite frontiers, man-made fences, and natural cliffs.  But consider what it means to reject cognition transcendence. Two theses from Normative Therapy were:

  • Motivation: normative structures should point towards their ends in motivationally-optimal ways.
  • Despair: It is not motivationally-optimal to be held to a normative structure beyond one’s capacities.

If these principles seem agreeable, it may be time to reject arguments of the form “all people should believe X”. 

Takeaways

In this post, we developed a metaphor of epistemic topography, or concept-space:

  1. A World Model Is A Location.
  2. The Reasoner Is A Vehicle
  3. Predictive Accuracy Is Height
  4. Intelligence Is Vehicular Speed
  5. Inference Is Travel
  6. Need For Cognition Is Frequency Of Travel

We then used this five-part metaphor to shed light on the following applications:

  • Education is the art of directing people whose locations you do not know towards higher peaks.
  • The Curse Of Knowledge can be explained as incomplete extrapolating from one’s own conceptual location.
  • The inferential journey can be blocked by three kinds of barriers: finite frontiers, man-made fences, and natural cliffs
  • These facts render arguments of the form “all people should believe X” dubious.

An Introduction To Category Theory [Part One]

kevinbinz Leave a comment

What’s So Important About Graphs?

Of all the conceptual devices in my toolkit, hyperpoints and graphs are employed the most frequently. I have explained hyperpoints previously; let me today explain What’s So Important About Graphs?

Human beings tend to divide the world into states versus actions. This metaphor is so deeply ingrained in our psyche that it tends to be taken for granted. Graphs are important because they visualize this state-action dichotomy: states are dots, actions are lines.

Put crudely, graphs are little more than connect-the-dots drawings. Now, dear reader, perhaps you do not yet regularly contemplate connect-the-dots in your daily life. Let me paint some examples to whet your appetite.

  1. Maps are graphs. Locations are nodes, paths are the edges that connect them.
  2. Academic citations are a graph. Papers are nodes, citations are the edges that connect them.
  3. Facebook is a graph. People are nodes, friendships are the edges that connect them.
  4. Concept-space is a graph. Propositions are nodes, inference are the edges that connect them.
  5. Causality is a graph. Effects are nodes, causes are the edges that connect them.
  6. Brains are graphs. Neurons are nodes, axons are the edges that connect them.

The above examples are rather diverse, yet we can reason about them within a single framework. This is what it means to consolidate knowledge.

Graph Theory: Applications & Limitations

It turns out that a considerable amount of literature lurks beneath each of our examples. Let’s review the highlights.

Once upon a time, Karl Popper argued that a scientific theory is only as strong as it is vulnerable to falsification. General relativity made the crazy prediction of gravitational lensing which was only later confirmed experimentally. One reason to call astrology “pseudoscience” is in its reluctance to produce such a vulnerable prediction.

But simple falsification doesn’t fully describe science: healthy theories can survive certain kinds of refutations. How? W. V. O. Quine appealed to the fact that beliefs cannot be evaluated in isolation; we must instead view scientific theories as a “web of belief”. And this web can be interpreted graphically! Armed with this interpretation, one can successfully evaluate philosophical arguments involving Quine’s doctrine (called confirmation holism) based on technical constraints on graphical algorithms.

The modern incarnation of confirmation holism occurs when you replace beliefs with degrees-of-belief. These probabilistic graphical models are powerful enough to formally describe belief propagation.

But even probabilistic graphical models don’t fully describe cognition: humans possess several memory systems. Our procedural memory (“muscle memory”) is a graph of belief, and our episodic memory (“story memory”) is a separate graph of belief.

How to merge two different graphs? Graph theory cannot compose graphs horizontally.

Switching gears to two other examples:

  • The formal name for brains-are-graphs is neural networks. They are the lifeblood of computational neuroscientists.
  • The formal name for Facebook-is-a-graph is social networks. They are vital to the research of sociologists.

How might a neuroscientist talk to a sociologist? One’s network represents the mental life of a person; the other, the aggregate lives of many people. We want to say is that every node in a social graph contains an entire neural graph.

How to nest graphs-within-graphs?  Graph theory cannot compose graphs vertically.

The Categorical Landscape

What are categories? For us, categories generalize graphs.

A directed graph can be expressed G = (V, E); that is, it contains a set of nodes, and a set of edges between those nodes.

A small category C = (O, M); that is, it contains a set of objects, and a set of morphisms between those objects.

Categories endow graphs with additional structure.

  1. Category Theory require the notion of self-loops: actions that result in no change.
  2. In Graph Theory, there is a notion of paths from one node to another. Category Theory promote every path into its very own morphism.
  3. Category Theory formalizes the notion of context: objects and morphisms live within a common environment; this context is called a “category”.

As an aside, directed graphs require only one edge between graphs, and no self-loops. We could tighten the analogy yet further by comparing categories to quivers (directed graphs that don’t forbid parallel edges and self-loops).

But enough technicalities. Time to meet to your first category! In honor of category theory’s mathematical background, allow me to introduce Set. In Set, objects are sets, and morphisms are functions. Here is one small corner of the category:
Category Theory- Set Category A (1)Self-loops 1A, 1B, and 1C change nothing; they are special kind of self-loops called identity morphisms. Since such things exist on every node, we will henceforth consider their existence implicit.

Recall our requirement that every path has a morphism. The above example contains three paths:

  • π1 = A → B
  • π2 = B → C
  • π3 = A → B → C

The first two paths are claimed by f and g, respectively, but the third is unaffiliated. For this to qualify as a category, we must construct for it a new morphism. How? We create h : A → C via function composition:

h(x) = g(f(x)) = [f(x)]-1 = 2x-1.

We also require morphism composition to be associative. Another example should make this clear:Category Theory- Set Category B

Besides g(f(x)), we can also write function composition as f●g (“f then g”). In the above, we have:

  • i(x) = f●g
  • j(x) = g●h
  • k(x) = f●g●h

With this notation, we express our requirement for morphism associativity as

  • k = (f●g)●h = f●(g●h).
  • That is, k = i●h = f●j.
  • That is, “you can move from A to D by travelling either along i-then-h, or along f-then-j”.

Harden The Definition

Let me be precise. Categories contain two types of data:

  1. A set of objects O.
  2. A set of morphisms M such that m : A → B

The set of morphisms is required to contain the following two sets:

  1. A set of identity morphisms 1 such that 1A : A → A
  2. A set of composition morphisms such that for every f : A → B and g: B → C, there is a morphism h: A → C.

The set of morphisms is required to respect the following two rules:

  1. Identity: composing a morphism with an identity does nothing.  f●1 = f = 1●f
  2. Associativity: the order in which you compose functions doesn’t matter. (f●g)●h = f●(g●h)

Connecting To Group Theory

Recall that groups define axioms governing set operations. A group might choose to accept or reject any of the following axioms:

  1. Closure
  2. Associativity
  3. Identity Element
  4. Inverse Element
  5. Associativity

We can now better appreciate our taxonomy from An Introduction To Group Theory:

Abelian- Other Group Types

Take a second to locate the Category group. Do you see how its two axioms align with our previous definition of a category?

Notice that in group theory, categories are kind of a degenerate monoid. Why have we removed the requirement for closure?

We can answer this question by considering the category SomeMonoid? It turns out that this category has only one object (with each of its member elements as self-loops). This is the categorical consequence of closure. We do not require closure in our category theory because we want license to consider categories with a multitude of objects.

Takeaways

In this article, I introduced graphs, and used human memory and social vs. neural networks to motivate two limitations of graph theory:

  1. How to merge two different graphs? Graph theory cannot compose graphs horizontally.
  2. How to nest graphs-within-graphs?  Graph theory cannot compose graphs vertically.

I then introduced you to Category Theory, showing how it both generalizes graph theory and connects to abstract algebra.

In the final half of this introduction, I will discharge my above two commitments. Specifically, next time I will show how:

  1. The concept of functor permits horizontal composition of categories.
  2. The distinction between “inside” and “outside” views facilitates vertical composition of categories.

The Structure Of Physics

kevinbinz Leave a comment

Part Of: Philosophy of Science sequence
Followup To: An Introduction To Structural Realism
Content Summary: 800 words, 8 min read

Motivations

Recall the takeaways from last time:

  1. Realists advance the no-miracles argument: the predictive power of science seems too implausible unless its theories somehow refer to reality.
  2. Anti-realists counter with pessimistic meta-induction: previously successful theories have been discarded; who are we to say that our current theories won’t meet the same fate.
  3. The approximation hypothesis is where these two arguments connect meaningfully: isn’t it more accurate to call older theories approximations rather than worthless?
  4. It is notoriously difficult to describe what “approximation” means.
  5. Some realists have conceded that scientific narratives tend to fail, but produce compelling evidence that scientific equations tend to persist. This position is known as structural realism (where formulae structure means more than the meaning of the variables).

This summary is all fine, until you start to wonder… what precisely does “formulae structure” mean? And how is such a thing approximated?

Vocabulary Sharpening

Before we begin, consider the word “approximate”. It is directional: while we can say that Newtonian Physics approximates General Relativity, such a statement casts the older theory as the actor. This temporal confusion helps no one. What’s worse, in my view, is that “approximation” hints at the end of science, as though our current theories are causally derived from some Ultimate Structure, some Theory Of Everything.

Physicists in the business of approximating quantum mechanics? No! Progress runs in the other direction.

New theories are “pulled up from” a Theory Of Everything? No! Theories are fueled by the earth… data is their breath.

Let us discard the notion of approximation and consider the reverse direction. We might cite “generalization” or “disaggregation” for this purpose. But let me instead use theory decompression.  Here is a sharper expression of the two tasks that lie before us:

  1. What is structure?
  2. How do scientists decompress structure?

The Language Of Categories

Category theory seems the best candidate for a realizer of structuralism.

What is category theory? I’m glad you asked!

  • Category theory divides the world in terms of objects and processes (and meta-processes, and meta-meta-processes, etc).
  • “Processes” are called morphisms, and “meta-processes” are called functors.
  • Meta-processes that inject new information into their target categories are called free functors, those that eject information are forgetful functors.
  • A category, then, looks a lot like a network graph – with morphisms connected various objects together.
    • How can a formula become a graph-like thing? Operations (*, +, etc) become morphisms, variables (x, y, etc) become objects.
  • One way to describe categories is by looking for patterns in the underlying “graph”. These patterns are known as universal constructions.
  • Categories earn adjectives for different combinations of universal constructions.
    • For example, any category equipped with a pattern known as “exponential” is called a closed category.

Categorical Interpretations Of Physics

In what follows, I will leverage some idea in (Baez/Stay 2009) Physics, Topology, Logic and Computation: A Rosetta Stone.

  • Of course, modern physics is composed of two separate theories: Quantum Field Theory, and General Relativity
  • Quantum Field Theory (QFT) is the category Hilb, which is a categorical interpretation of a Hilbert space.
  • General Relativity (GR) is the category nCob, which is a categorical interpretation of the topological notion of cobordism.
  • Both QFT and GR both share the same set of patterns, and hence they share the same adjectives. Both are closed symmetric monoidal categories.
    • Noticing the pattern overlap is now motivating work towards a unified [Physics] Theory Of Everything.
    • As an aside, do you know what other categories share this moniker? Computation and linear logic.
  • Newtonian Physics is the category Vec, which is a categorical interpretation of vector space. It is not closed symmetric monoidal.
    • Note: unlike the rest of this section, take the above line with buckets of salt. It is my own conjecture, used for illustrative purposes.
  • In this setting, what is the meaning of theory decompression? Such a thing might be the construction of free functors, i.e., decompression functors.

Structural Realism- Disapproximation

I intend to flesh out this present section in the coming years. But for now, here is where we leave it.

Harden Your Query

We have successfully hardened the concept of structure, and used it to harden our theory of physics. Consider again our second question:

  • How do scientists decompress structure?

With our newfound understanding of structure, we can make this research question more precise:

  • How does Vec produce the same predictions as Hilb + nCob?
  • How do scientists go about constructing decompression functors?

Category theory is not yet powerful enough to answer these questions. They are, I submit, the most important unsolved questions in all of philosophy of science.

Wrapping Up

Let me close on a note of poetry. The following quote is one of the most beautiful thoughts I have ever encountered. It is attributed to Stephen Hawking.

What is it that breathes fire into the equations and makes a universe for them to describe?

For us, our query has become:

What is it that breathes fire into these categories and makes a universe for them to describe?

[Sequence] Philosophy of Science

kevinbinz Leave a comment

Structural Realism- Disapproximation

The first three posts of this sequence set up two important challenges facing modern science:

  • How do scientists go about decompressing structure?
  • Can category theory absorb the field of statistics?

The final post of this sequence suggests that these questions are in fact, the same.

Article List

  1. An Introduction To Structural Realism
  2. The Mathematical Structure Of Physics
  3. On Bridging The Archipelago
  4. The Microcosm Of Computer Science

An Introduction To Structural Realism

kevinbinz Leave a comment

Part Of: Philosophy of Science sequence
Content Summary: 900 words, 9 min read

Does science describe the world? Let me frame this foray into philosophy of science as a dialectic.

The Exchange

It is a brisk spring evening, just before sunset. Achilles and the Tortoise are taking their ritualized evening stroll down a winding country road. Their discussions vary wildly, but typically center around some current events or some random bit of science news.

  • Achilles comments out of the blue: “Tortoise, I can’t help but notice that you seem to place too much weight in scientific claims.”
  • “Do you really doubt the existence of the electron?” the Tortoise counters. “I mean, if particle physics got that wrong, then how could it wield such predictive power?”
  • Achilles’ pace slows, as he puzzles over the Tortoise’s reply. “But doesn’t it strike you as arrogant to believe we were lucky enough to be born in an age where science got it right? I would probably credit my skepticism to my reading of scientific history, at watching long lines of scientific theories crumble and fall.”
  • Tortoise replies: “Achilles, I have a slogan I like to tell people, to explain my way of thinking. When people thought the earth was flat, they were wrong. When people thought the earth was spherical, they were wrong. But if you really think that thinking the earth is spherical is just as wrong as thinking the earth is flat, then your view is wronger than both of them put together.”
  • Tortoise continues: “My point is simply that your binary notion of truth must become more subtle. It seems better to say that modern theories (such as general relativity) approximate older theories (like Newtonian mechanics).”

Now,  in case you haven’t heard these arguments before, Achilles is Thomas Kuhn and Tortoise is Isaac Asimov. I have found the appeal to approximation compelling, and so (I submit) do most scientists. However, here is the depth at which most people stop. Let us instead swim further… let us listen more carefully to Achilles.

  • Achilles gathers his thoughts. “When you read your textbooks, Tortoise, how many hours do you spend perusing the history section?”
  • “Not many, Achilles.” The Tortoise seems neither apologetic nor proud of this fact. “While Tortoises do in fact live for 200 years, my time is still finite. I’d rather let my mind reside near the state of the art.”
  • “Of course learning about history is not for everyone, Tortoise… but I have. Consider what it would feel like to read science textbooks from my eyes. Naturally enough, these texts are written by the victors of scientific disputes… but their history sections without fail do violence to the actual thinking of their predecessors.” Achilles’ speech is picking up speed. “Tortoise, if you study history like I do, your nose would smell propaganda, as mine does.”
  • Achilles drives his point home: “Shouldn’t this stench give you pause, Tortoise?  Your claim about scientific revolutions approximating their predecessors strikes you as intuitive, but do historians concur? In fact, you stand at odd with the facts of scientific revolutions. General relativity was not conceived as a generalization of classical mechanics. What relativistic concept does the Newtonian concept of simultaneity ‘approximate’? It does not! Consider also the ether. It was not approximated, it was trashed! Your notion of approximation seems misguided, my friend.”

This is the Kuhnian critique of scientific realism. Most philosophers consider the strongest reply to go as follows:

Startled at his inability to defend his vague notions, Tortoise spends the next several months studying scientific histories, and trying to improve his theory of approximation. Spring turns into summer… but then one day, Tortoise feels ready to return to this topic:

  • “Achilles, do you remember our conversation about scientific histories?”
  • “Of course I do, Tortoise!”
  • “Well, It seems to me that you’ve put your finger on something important. I’ve spent time poring over memoirs of past intellectual giants as you have, and I definitely now see what you mean by the ‘smell of propaganda’. But Achilles, I think I’ve noticed something else, something important”.
  • Tortoise continues: “When I look at the debates between competing theories, my cherished notion of approximation cannot be resuscitated. But! When I compare the equations of new theories to the ones they replace, I do see an approximation. For example, I cannot recover the Newtonian dogma of flat three-dimensional space, but if I assume the speed of light is infinite, I can recover the Newtonian equation of gravity directly from general relativity.”
  • Tortoise concludes: “Achilles, it seems to me that the only continuity in science is in its laws. I will no longer claim to know that electrons are real, or that spacetime is curved. Concepts may not refer. It is only the relationship between concepts, the formal structure of a mature theory, that lasts”.

Condensing The Argument

The above conversation is based on (Worrall, 1989) Structural Realism: The Best Of Both Worlds?. We can compress the above as follows:

  1. Realists advance the no-miracles argument: the predictive power of science seems too implausible unless its theories somehow refer to reality.
  2. Anti-realists counter with pessimistic meta-induction: previously successful theories have been discarded; who are we to say that our current theories won’t meet the same fate.
  3. The approximation hypothesis is where these two arguments connect meaningfully: isn’t it more accurate to call older theories approximations rather than worthless?
  4. It is notoriously difficult to describe what “approximation” means.
  5. Some realists have conceded that scientific narratives tend to fail, but produce compelling evidence that scientific equations tend to persist. This position is known as structural realism (where formulae structure means more than the meaning of the variables).

Metaphor Is Narrative

kevinbinz Leave a comment

The Nature Of Metaphor

Just for fun, let me open today’s discussion with a few aphorisms:

  1. It feels more natural to say “her smile is warm” than “her body warmth is a smile”. Metaphor is asymmetrical. 
  2. Abstraction is wedded to metaphor.
  3. Inference flows from the concrete to the abstract. Metaphor relocates inference.
  4. The flow of inference is constrained. When we say “that lawyer is a shark” our brains decide which of our shark inferences are relevant.
  5. Idiom is a form of metaphor. Like idiom, metaphor can go stale.
  6. Metaphor relocates affect, even after the stream of inference dries up.
  7. Metaphor imbues communication with affective flair or style.
  8. Metaphors are hierarchical, with complex themes (e.g., “a Purposeful Life is a Journey”) made of smaller metaphors.
  9. In my language, I say that metaphor is narrative. That is, weaving metaphorical hierarchies is narrative paint.
  10. Metaphor is not yet differentiated sufficiently to compose well with the rest of cognitive science.

Primary Sensorimotor Metaphor

Okay, time to delve a little deeper. Consider the following metaphors.

  1. Affection Is Warmth (“her smile is warm”)
  2. Important is Big (“tomorrow is a big day”)
  3. Happy Is Up (“I feel uplifted”)
  4. Intimacy Is Closeness (“we’re beginning to drift apart”)
  5. Bad Is Stinky (“this artist stinks”)
  6. Difficulties Are Burdens (“finals are weighing me down”)
  7. More Is Up (“prices are high”)
  8. Categories Are Containers (“do tomatoes go in the fruit category?)
  9. Similarity Is Closeness (“these colors are close”)
  10. Linear Scales Are Paths (“your IQ goes well beyond mine”)
  11. Organization Is Physical Structure (“how do the pieces of this theory fit together”)
  12. Help Is Support (“support your local charity”)
  13. Time Is Motion (“time flies”)
  14. States Are Locations (“close to having an anxiety attack”)
  15. Change Is Motion (“car has gone from bad to worse”)
  16. Actions Are Self-Propelled Motions (“my project is moving along”)
  17. Purposes Are Destinations (“I’m not where I wanted to be”)
  18. Purposes Are Desired Objects (“grab the opportunity”)
  19. Causes Are Physical Forces (“pushed the bill through Congress”)
  20. Relationships Are Enclosures (“this feels confining”)
  21. Control Is Up (“I’m on top of it”)
  22. Knowing Is Seeing (“see what you mean”)
  23. Understanding Is Grasping (“gotten my mind around imaginary numbers”)
  24. Seeing Is Touching (“pick my face out of the crowd”)

What similarities between these metaphors do you see? [Footnote 1] Well, these questions are all unidirectional, and explain abstract concepts by appealing to more down-to-earth domains. What do I mean by down-to-earth? Well, all of the above examples appeal to perceptual or motor phenomena!

In terms of the human brain, perceptual and motor (“sensorimotor”) systems tend to reside in the cortical homunculus. In terms of the human memory hierarchy, these types of concepts tend to arise in procedural memory.

Primary Metaphor In Other Memory Systems

Now, human memory contains more than just procedural memory. We can use our understanding of other memory systems to predict other kinds of primary metaphor.

  • “Lawyers are sharks” might be better explained by appealing to a culturally-ubiquitous item of semantic memory
  • The Biblical metaphor “Sinners are tax collectors” would plausibly draw from a culturally-ubiquitous item of episodic memory.
  • Since autobiographical memories are not culturally ubiquitous, we might predict a more personal taste to this type of metaphor.

Metaphor Composition Is Narrative Paint

Human beings conceptualize abstract objects by bringing many primary metaphors into a complex whole. Let me pull an example from Lakoff & Johnson: the concept of Time [Footnote 2].

The Time Orientation Metaphor looks like this:

  • The Location Of The Observer → The Present
  • The Space In Front Of The Observer → The Future
  • The Space Behind The Observer → The Past

Examples: That’s all behind us now. We’re looking forward to your presentation. He has a great future in front of him.

The Moving Time Metaphor interprets times to be objects and the passage of time to be the motion of objects past the observer.  This metaphor really finds its legs when composed with the Time Orientation metaphor. The Time Orientation + Moving Time complex metaphor, then, looks like this:

  • The Location Of The Observer → The Present
  • The Space In Front Of The Observer → The Future
  • The Space Behind The Observer → The Past
  • Objects → Times
  • Motion Of Objects Past The Observer → The “Passage” Of Time

Examples: The time will come when there are no more typewriters. The time has long since gone when you could mail a letter for three cents. The time for action has arrived. Thanksgiving is coming up on us. Time is flying by. Let’s meet the future head-on.

But abstractions like time are typically underwritten by more than one can of narrative paint. In this case, the Moving Observer Metaphor alternatively imagines location on the observer’s path as times, and the motion of the observer as the passage of time. Here is the Time Orientation + Moving Observer complex metaphor, in full detail:

  • The Location Of The Observer → The Present
  • The Space In Front Of The Observer → The Future
  • The Space Behind The Observer → The Past
  • Locations On Path Observer’s Path   → Times
  • Motion Of The Observer → The “Passage” Of Time
  • Distance Moved By Observer → The Amount Of Time “Passed”

Examples: There’s going to be trouble down the road. What will be the length of his visit? Let’s spread the conference over two weeks. We passed the deadline. We’re halfway through September. His visit to Russia extended over many years.

Takeaways

Today, I gave you examples of “primary” metaphor, which in this case were grounded in the human perceptual/motor systems. Abstract concepts are made by gluing primary metaphors together like Legos. I also left you with several aphorisms, including:

  • Metaphor relocates inference.
  • Metaphor imbues communication with affective flair or style.
  • Weaving metaphorical hierarchies is narrative paint.

Footnotes

  1. This question (“do you see”) nicely illustrates primary sensorimotor metaphor #22.
  2. Source: http://www.amazon.com/Philosophy-Flesh-Embodied-Challenge-Western/dp/0465056741. For reasons outside the scope of this post, I cannot endorse this text, but I did find its presentation of complex metaphor useful.