Author kevinbinz

An Introduction to Topology

kevinbinz Leave a comment

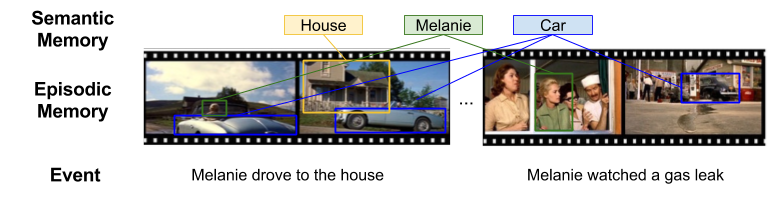
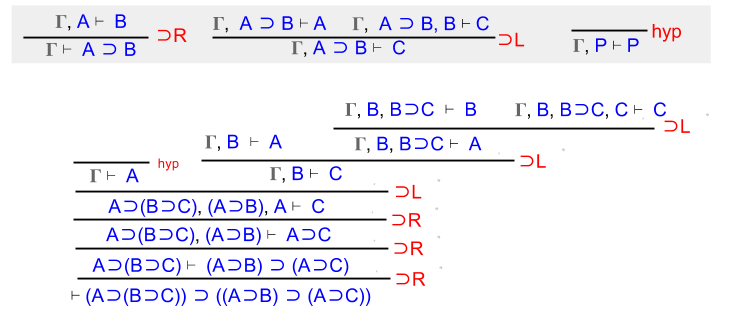
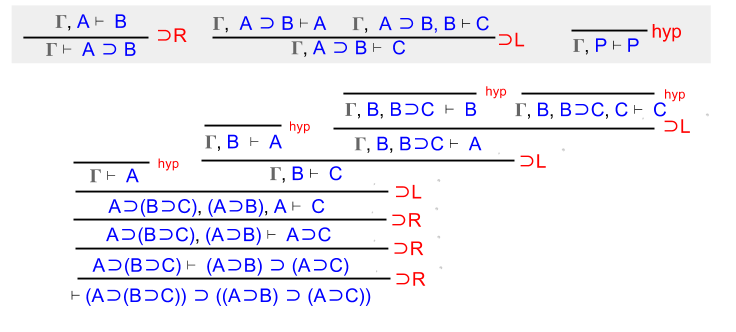
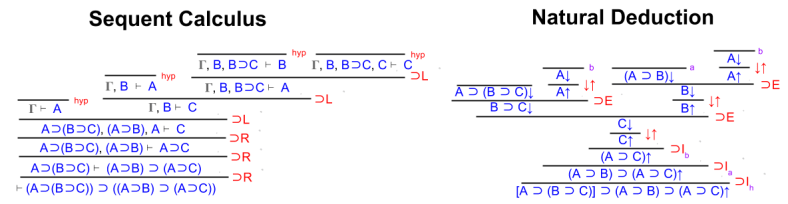
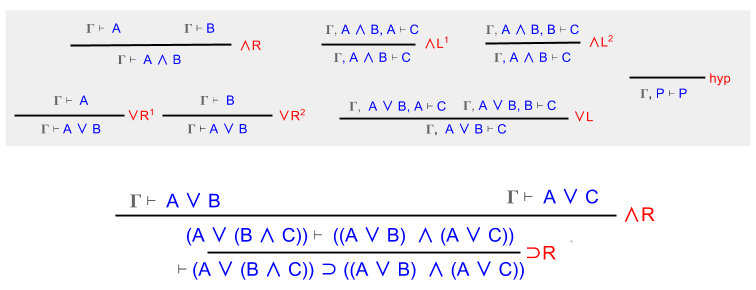
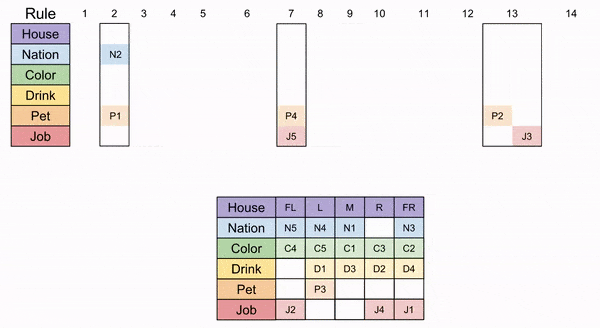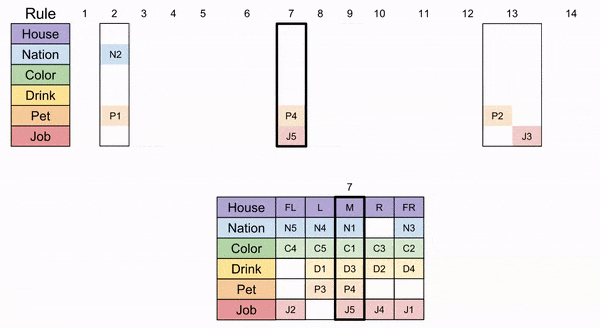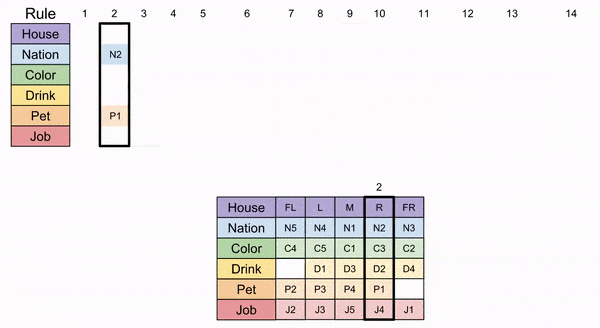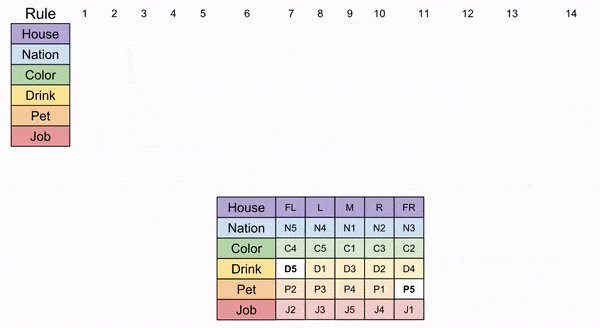
Part Of: Analysis sequence
Content Summary: 1000 words, 10 min read

Motivating Example

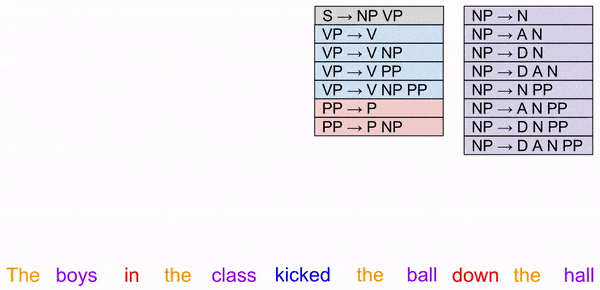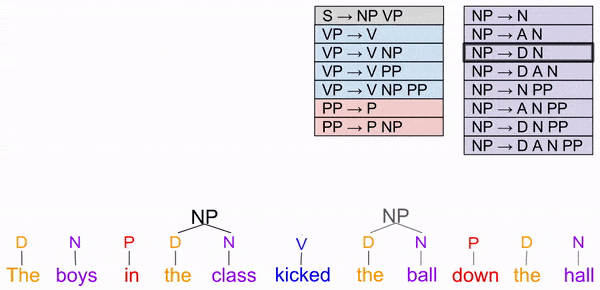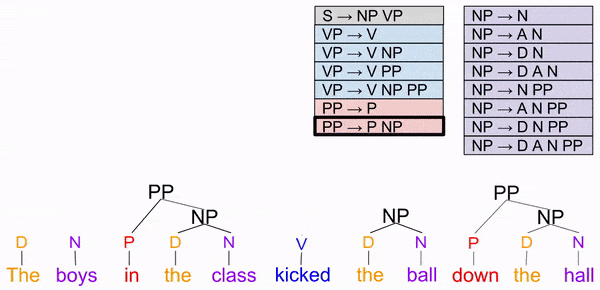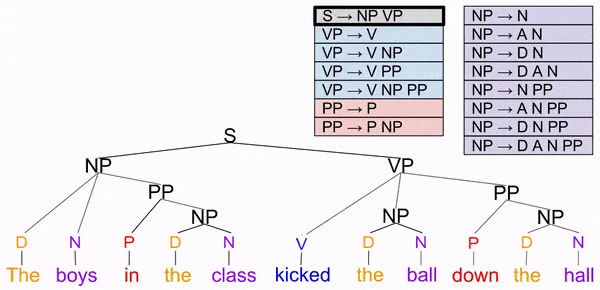
Can you draw three lines connecting A to A, B to B, and C to C?  The catch: the lines must stay on the disc, and they cannot intersect.

Topology- Motivating Problem (2)

Here are two attempts at a solution:

Topology- Potential Solutions (1)

Both attempts fail. In the first, there is no way for the Bs and Cs to cross the A line. In the second, we have made more progress… but connecting C is impossible.

Does any solution exist? It is hard to see how…

Consider a simplified puzzle. Let’s swap the inner points B and C.

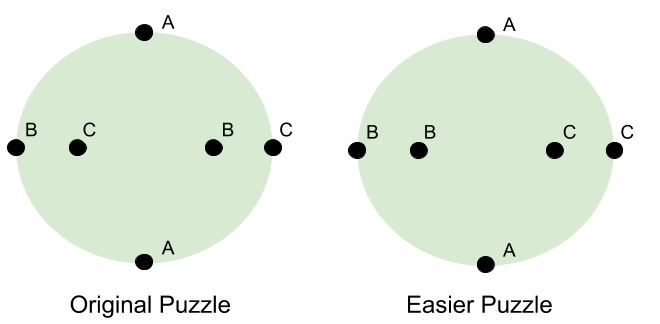
Topology- Original vs Easy Puzzle (2)

In the new puzzle, the solution is easy: just draw straight lines between the pairs!

To understand where this solution breaks down, let’s use continuous deformation (i.e., homeomorphism) to transform this easier puzzle back to the original. In other words, let’s swap point B towards C, while not dropping the “strings” of our solution lines:

topology

Deformation has led us to the solution! Note what just happened: we solved an easy problem, and than “pulled” that solution to give us insight into a harder problem.

As we will see, the power of continuous deformation extends far beyond puzzle-solving. It resides at the heart of topology, one of mathematics’ most important disciplines.

Manifolds: Balls vs Surfaces

The subject of arithmetic is the number. Analogously, in topology, manifolds are our objects. We can distinguish two kinds of primitive manifold: balls and surfaces.

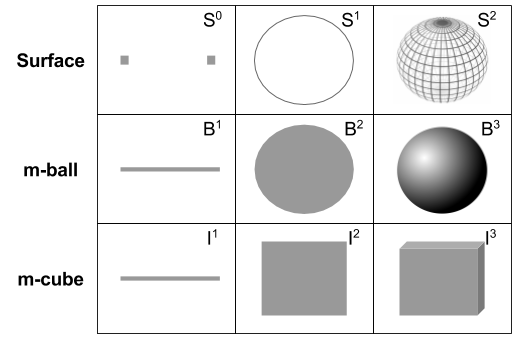
Topology- Balls and Surfaces (1)

These categories generalize ideas from elementary school:

  • A 1-ball B^1 is a line segment
  • A 2-ball B^2 is a disc
  • S^1 is a circle
  • S^2 is a sphere

Note the difference between volumes and their surfaces. Do not confuse e.g., a disc with a circle. The boundary operation \partial makes the volume-surface relationship explicit. For example, we say that \partial B^2 = S^1.

Note that surfaces are one dimension below their corresponding volume. For example, a disc resides on a plane, but a circle can be unrolled to fit within a line.

Importantly, an m-ball and an m-cube are considered equivalent! After all, they can be deformed into one another. This is the reason for the old joke:

A topologist cannot tell the difference between a coffee cup and a donut. Why? Because both objects are equivalent under homeomorphism:

coffeetodonut

If numbers are the objects of arithmetic, operations like multiplication act on these numbers. Topological operations include product, division, and connected sum. Let us address each in turn.

On Product

The product (x) operation takes two manifolds of dimension m and n, and returns a manifold of dimension m+n. A couple examples to whet your appetite:

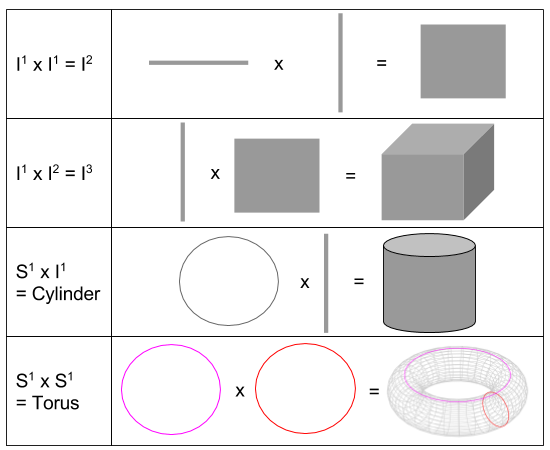
Topology- Examples of Product (1)

These formulae only show manifolds of small dimension. But the product operation can just as easily construct e.g. a 39-ball as follows:

B^{39} = \prod_{i=1}^{39} I^1

How does product relate to our boundary operator? By the following formula:

\partial (M x N) = ( \partial M x N) \cup (M x \partial N )

This equation, deeply analogous to the product rule in calculus, becomes much more clear by inspection of an example:
Topology- Product vs Boundary (1)

On Division

Division ( / ) glues together the boundaries of a single manifold. For example, a torus can be created from the rectangle I^{2}:

torus_by_division

We will use arrows to specify which edges are to be identified. Arrows with the same color and shape must be glued together (in whatever order you see fit).

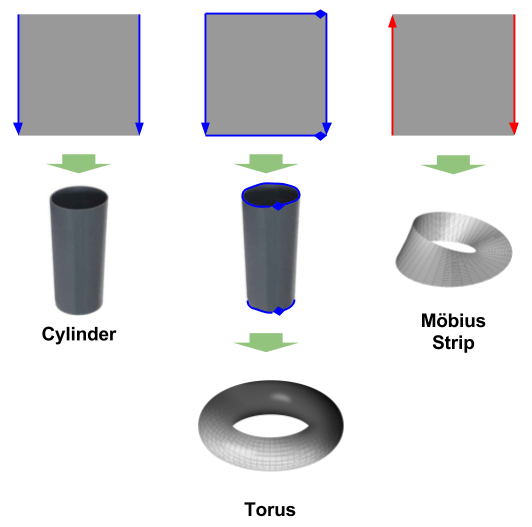
Topology- Division Simple Examples (2)

Alternatively, we can specify division algebraically. In the following equation, x=0 means “left side of cylinder” and x=1 means right side:

S^1 x I^1 = Cylinder = \frac{I^2}{(0,y) \sim (1, y) \forall y}

The Möbius strip is rather famous for being non-orientable: it neither has an inside nor an outside. As M.C. Escher once observed, an ant walking on its surface would have to travel two revolutions before returning to its original orientation.

More manifolds that can be created by division on I^{2}. To construct a Klein bottle by division, you take a cylinder, twist it, and fold it back on itself:

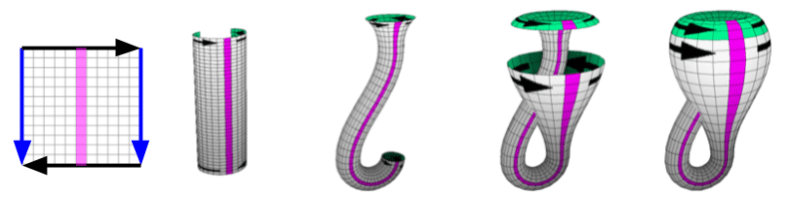
Topology- Klein Bottle Construction (5)

In our illustration, there is a circle boundary denoting the location of self-intersection. Topologically, however, the Klein bottle need not intersect itself. It is only immersion in 3-space that causes this paradox.

Our last example of I^{2} division is the real projective plane RP^{2}. This is even more difficult to visualize in 3-space, but there is a trick: cut I^{2} again. As long as we glue both pieces together along the blue line, we haven’t changed the object. 

Topology- Deriving Real Projective Plane First Part (1)

The top portion becomes a Möbius strip; the bottom becomes a disc. We can deform a disc into a sphere with a hole in it. Normally, we would want to fill in this hole with another disc. However, we only have a Möbius strip available.

But Möbius strips are similar to discs, in that its boundary is a single loop. Because we can’t visualize this “Möbius disc” directly, I will represent it with a wheel-like symbol.  Let us call this special disc by a new name: the cross cap.

The real projective plane, then, is a cross cap glued into the hole of a sphere.  It is like a torus; except instead of a handle, it has an “anomaly” on its surface.

Topology- Deriving Real Projective Plane Second Part

These then, are our five “fundamental examples” of division:

Topology- Division Overview (3)

On Connected Sum

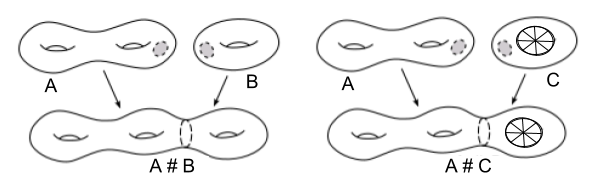
Division involves gluing together parts of a single manifold. Connected sum (#), also called surgery, involves gluing two m-dimensional manifolds together. To accomplish this, take both manifolds, remove an m-ball from each, and identify (glue together) the boundaries of the holes. In other words:

\frac{ ( M_1 / B_1 ) \cup ( M_2 / B_2 ) }{ \partial ( M_1 / B_1 ) \sim \partial ( M_2 / B_2 )} = M_1 \# M_2

Let’s now see a couple examples. If we glue tori together, we can increase the number of holes in our manifold. If we attach a torus with a real projective plane, we acquire a manifold with holes and cross-cuts.
Topology- Connected Sum examples (3)

Takeaways

  • Topology, aka. “rubber sheet geometry”, is the study of malleable objects & spaces.
  • In topology, manifolds represent objects in n-dimensional space.
  • Manifolds either represent volumes (e.g., disc) and boundaries (e.g., circles)
  • Manifolds are considered equivalent if a homeomorphism connects them.
  • There are three basic topological operations:
    • Product (x) is a dimension-raising operation (e.g., square can become a cube).
    • Division (/) is a gluing operation, binding together parts of a single manifold.
    • Connected sum (#) i.e., surgery describes how to glue two manifolds together.

Related Materials

This post is based on Dr. Tadashi Tokeida’s excellent lecture series, Topology & Geometry. For more details, check it out!

The X-Bar Theory of Phrase Structure

kevinbinz 2 Comments

Part Of: Language sequence
Followup To: An Introduction to Generative Syntax
Content Summary: 800 words, 8 min read

Explaining Substitution

Consider the sentence “I bought this big book of poems with the red cover”.

XBar- Flat Noun Phrase (1)

In everyday language, we often replace words and phrases with indexing words like “one”. Call this indexing replacement.The meaning of these words can be obtained from the context.

At first glance, indexing replacement seems to target a branch in the syntax tree. For example:

  • I bought that big one of poems with the red cover (“one” replaces the noun)
  • I bought one (“one” replaces the entire noun phrase)

But there are several other substitutions don’t follow from branch replacement:

  • I bought that big one.
  • I bought that small one
  • I bought that big one of poems with the blue cover

Perhaps our notion of noun phrases is too flat. Perhaps we need additional nodes to describe structure within the noun phrase. We will call these intermediate nodes N’, (where N → N’ → N’’ = NP):

towards_noun-bar

This new tree successfully predicts all substitution phenomena, by modeling “one” as replacing various “N-bar” nodes:

xbar_noun_substitution

We can similarly introduce depth to our verb phrases (VPs), by using intermediate V’ (“V-bar”) nodes:

XBar- Verb Substitution (2)

The X-Bar syntax tree provides a simple explanation of the “do so” substitution effects:

  • I will do so in the office before the party.
  • I will do so before the party.
  • I will do so.

A General Theory of Phrases

We can revise our original NP and VP rules to reflect our intermediate N’ and V’ nodes:

Xbar Theory- Towards XBar Rules

What if noun and verb phrases are instantiations of a more general phrase structure? Just as group theory identifies overlap in the axioms of addition and subtraction, X-bar theory explores the similarity between NP and VP rules.  

Xbar Theory- XBar Parameterization (1)

There are only four kinds of phrase constituents:

  1. The head carries the central meaning of the phrase. Consider the sentence “The tall student who is wearing the red shirt asked questions of her professor, after the lecture.” The central meaning is retained if we remove all non-head words: “student asked questions”.
  2. The specifier points to the head. For nouns, specifiers include determiners (“the”) and possessives (“her”). For verbs, adverbs occasionally fill this role (“quickly”).
  3. The complement tends to feel intimately related to the head of a phrase (e.g., “of poems” in “a book of poems”).
  4. Adjuncts, on the other hand, tend to feel more optional (e.g., “big” in “big book”).

Xbar Theory- Phrase Structure

Adjuncts vs Complement

Given that adjuncts and complements both often inhabit prepositional phrases, it is perhaps surprising that they should behave differently. The distinction between adjuncts and complements explains why this should be the case. Let us look at four behavioral differences:

Difference #1. Adjuncts can be reordered freely. 

Consider our example verb phrase:

Xbar Theory- VBar and NBar Example

This rule means that our two adjuncts can be shuffled, but the complement NP must retain its original position

  • I will read the letter in the office before the party (Original order: valid)
  • I will read the letter before the party in the office (Adj reorder: valid)
  • *I will read in the office before the party the letter (Compl reorder: invalid)

Difference #2. Indexing replacement cannot strand the complement.

For example,

  • I will do so in the office before the party (Adj is stranded: valid)
  • *I will do so the letter before the party (Compl is stranded: invalid)

Consider another part of speech we have not yet considered: conjunction words like “and” and “or”.

Difference #3. Conjunction words bind adjuncts together, and complements together. But adjunct-complement bindings are non-grammatical.

Consider our example noun phrase:

Xbar Theory- NBar Example (1)

Three examples to illustrate how conjunction works:

  • I bought the book of poems and of short stories. (Compl-compl conjunction: valid)
  • The book with the red cover and the black spine. (Adj-adj conjunction: valid)
  • *The book of poems and with the red cover. (Compl-adj conjunction: invalid)

What X-Bar Theory Tells Us About Memory

Earlier, I introduced the distinction between episodic and semantic memory:

  • Semantic: ability to remember facts and concepts (e.g., hands have five fingers)
  • Episodic: ability to remember events or episodes (e.g., dinner last Tuesday night)

Concepts are learned by extracting commonalities from episodic memories. If you see enough metallic blocks moving around on four cylinders, you’ll eventually consolidate these objects into the CAR concept:

XBar Theory- Semantic vs Episodic Memory

In philosophy, I suspect the concepts of necessity and contingency relate to semantic and episodic memory, respectively.

In linguistics, I suspect complements help locate concepts in semantic memory, whereas adjuncts assist episodic localization. In the sentence “I bought the book of poems with the red cover”, the complement helps us activate the concept POEM-BOOK, whereas the adjunct creates sense-predictions that locate it within our episodic memory.

Takeaways

  • With flat syntax trees, it is difficult to explain indexing substitution (e.g., “bought a book” → “bought one”)
  • If we make syntax trees binary, by introducing intermediate  X’ (“X-Bar”) nodes, substitution becomes more straightforward.
  • Noun and verb phrases thus parameterize a more general phrase structure.
  • Phrases have four kinds of constituents: head, specifier, complement, and adjuncts.
  • The differences between complements and adjuncts are instructive:
    • Only adjuncts can be reordered.
    • Indexing replacement cannot strand the complement.
    • Conjunction cannot bind across categories
  • In human cognition, complements and adjuncts may correspond to semantic and episodic memory, respectively.

An Introduction to Generative Syntax

kevinbinz Leave a comment

Part Of: Language sequence
Content Summary: 900 words, 9 min read

Syntax vs Semantics

In language, we distinguish between syntax (structure) and semantics (meaning).

Compare the following:

  • “Colorless green ideas sleep furiously”
  • “Sleep ideas colorless green furiously”

Both sentences are nonsensical (a semantic transgression). But the first is grammatically correct, whereas the second is malformed.

The brain responds differently to errors of syntax and semantics, as measured by an EEG machine. Semantic errors produce a negative voltage after 400 milliseconds (“N400”); syntactic errors produce a positive voltage after 600 milliseconds (“P600”):

Syntax- Linguistic ERPs (1)

Parts of Speech

To understand syntax more precisely, we must differentiate parts of speech. Consider the following categories:

  • Noun (N).  cat, book, computer, peace, …
  • Verb (V). jump, chase, eat, sleep, …
  • Adjective (A). long, purple, young, old, …
  • Determiner (D) the, this, many, all, …
  • Preposition (P) in, on, to, for, with…

Nouns and verbs correspond to perception- and action- representations, respectively. They are an expression of the perception-action cycle. But to study syntax, it helps to put aside semantic context, and explore how parts of speech relate to one another.

Phrases as Color Patterns

To understand syntax intuitively, start by adding color to sentences.  Then try to find patterns of color unique to well-formed sentences.

Let’s get started!

Syntax- Noun Phrase Abstraction (3)

“Noun-like” groups of words appear on either side of the verb. Let noun phrase (NP) denote such a group. Optional parts of speech are indicated by the parentheses. Thus, our grammar contains the following rules:

  1. S → NP V NP
  2. NP → (D) (A) N

These rules explain why the following sentences feel malformed:

  • “Chase dogs cats” (violates rule 1)
  • “Old some dogs chase cats” (violates rule 2)

But these rules don’t capture regularities in how verbs are expressed. Consider the following sentences:

Syntax- Verb Phrase Abstraction (1)

A verb phrase contains a verb, optionally followed by a noun, and/or a preposition.

  1. S → NP VP
  2. NP → (D) (A) N
  3. VP → V (NP) (P NP)

This is better. Did you notice how we improved our sentence (S) rule? 🙂 Subject-only sentences (e.g. “She ran”) are now recognized as legal.

Prepositions are not limited to verb phrases, though. They also occur in noun phrases. Consider the following:

Syntax- Prepositional Phrase Abstraction

Prepositions are sometimes “attached to” a noun phrase. We express these as a prepositional phrase, which includes a preposition (e.g. “on”) and an optional noun phrase (e.g. “the table”).

  1. S → NP VP
  2. NP → (D) (A) N (PP)
  3. VP → V (NP) (PP)
  4. PP → P (NP)

Notice how we cleaned up the VP rule, and improved the NP rule.

Congratulations! You have discovered the rules of English. Of course, a perfectly complete grammar must include determiners (e.g., “yours”), conjunction (e.g., “and”), interjection (e.g., “wow!”). But these are fairly straightforward extensions to the above system.

These grammatical rules need not only interest English speakers. As we will see later, a variant of these rules appear in all known human languages. This remarkable finding is known as universal grammar. Language acquisition is not about reconstructing syntax rules from scratch. Rather, it is about learning the parameters by which your particular natural language (English, Chinese, Egyptian) varies from the universal script.

From Rules to Trees

Our four rules are polymorphic: they permit more than one kind of structure. Unique rule sets are easier to analyze, so let’s translate our rules into this format:

Syntax- Compressed vs Unique Ruleset (1)

 

Importantly, we can conceive of these unique rules as directions to construct a tree. We can conceive of the sentence “Dogs chase cats” as:

Syntax- Simple Tree (1)

Sentences are trees. These trees are not merely used to verify whether grammatical correctness. They play a role in speech production: which transforms the language of thought (Mentalese) to natural language (e.g., English). For more on this, see my discussion of the Tripartite Mind.

How can (massively parallel) conscious thought be made into (painfully serial) speech utterances? With syntax! Simply take the concepts you desire to communicate, and construct a tree based on (a common set of) syntactical rules.

syntax_tree_construction

Tree construction provides much more clarity on the phenomena of wordplay (linguistic ambiguity). Consider the sentence “I shot a wolf in my pajamas”. Was the gun fired while you were wearing pajamas? Or was the wolf dressed in pajamas?

Syntax- Multiple Interpretation Ambiguity

Both interpretations agree on parts of speech (colors). It is the higher-order structure that admits multiple choices. In practice, semantics constrain syntax: we tend to select the interpretation is feels the most intuitive.

The Sociology of Linguistics

The above presentation uses a simple grammar, for pedagogic reasons. I will at some point explain the popular X’ theory (pronounced “X bar”), which explores similarities between different phrase structures (e.g., NP vs PP). Indeed, there is a wide swathe of possible grammars that we will explore.

Syntax- Sociology of Linguistic Research

Generative grammar is part of the Symbolist tribe of machine learning. As such, this field has rich connections with algebra, production systems, and logic. For example, propositional logic was designed as the logic of sentences; predicate logic is the logic of phrases.

Other tribes besides the Symbolists care about language and grammar, of course. Natural Language Processing (NLP) and computational linguistics have been heavily influenced by the Bayesian tribe, and use probabilitic grammars (i.e., PCFGs).

More recently, the Connectionist tribe (and deep learning technologies) are taking a swing at producing language. In fact, I suspect neural network interpretability will only be achieved once a Connectionist account of language production has matured.

Takeaways

  • Language can be understood via syntax (structure) and semantics (meaning).
  • Syntax requires delineating parts of speech (e.g., nouns vs verbs).
  • Parts of speech occur in patterns called phrases. We can express these patterns as the rules of syntax.
  • Sentences are trees. Syntax rules are instructions for tree construction.
  • Sentence-trees provide insight into problems like sentence ambiguity.

For more resources on syntax trees, I recommend this lecture, this website, and this Youtube channel.

Until next time.

Logic Inference: Sequent Calculus

kevinbinz Leave a comment

Part Of: Logic sequence
Followup To: Natural Deduction
Content Summary: 600 words, 6 min read

Motivating Sequent Calculus

Last time, we labelled propositions in the language of verification.

  • ↑ represents conjecture: propositions that require verification
  • ↓ represents assumption: propositions that can be used for verification.

Two of our connective rules (⊃I and ∨E) expanded our set of assumptions, which we could use at any later time. Logic acumen is invoking the right assumption at the right time.

In contrast to natural deduction, sequent calculus explicitly tracks the set of assumptions) as they vary across different branches of the proof tree.

We will use the turnstile to distinguish assumptions from conjecture: { assumptions } ⊢ { conjectures }

In natural deduction, progress in bidirectional: we are done when we found a connection between assumptions and conjecture. In sequent calculus, progress is unidirectional. Instead, we start with no assumptions, and finish when we have no conjectures left to demonstrate.

Sequence Calculus- Different Schematics (1)

Both logical systems rely on two sets of five rules. They bear the following relationships:

  • R = I. Right rules are very similar to Introduction rules.
  • L = E-1. Left rules must be turned “upside down”.

Right and Left rules

We here define capital gamma Γ to represent the context, or current set of assumptions.

Right rules simply preface Introduction rules with  “Γ ⊢”. The exception ⊃R is instructive. There, A is added to the context, and our “target” conjecture shrinks to just B.
Sequent Calculus- Right vs Introduction (2)

Left rules are less transparently related to Elimination. They are more easily understood by an English explanation:

Sequent Calculus- Left Rule English Interpretation (2)

The entire structure of sequent calculus, then, looks like this:

Sequent Calculus- Left and Right Rules (1)

Enough theory! Let’s use sequent calculus to prove stuff.

Example 1: Implication

Show that (A ⊃ (B ⊃ C)) ⊃ ((A ⊃ B) ⊃ (B ⊃ C)).

Here, ⊃R serves us well:

Sequent Calculus- Implication Step0 (1)

We have parsed the jungle of connectives, and arrived at a clear goal. We need to prove C. How?

Recall what ⊃L means: “if you have assumed A ⊃ B, you may also assume B (right branch) if you can prove A with your current assumptions (left branch).

Let’s apply ⊃L to the A ⊃ B proposition sitting in our context. To save space, let us here define Γ with the following three elements: { A⊃(B⊃C), A⊃B, and A }.

Sequent Calculus- Implication Step1.png

We can solve the left branch immediately. Since A ∈ Γ, we can invoke the hyp rule.

Unfortunately, assuming B is not enough to prove C. We must invoke ⊃L again, this time against our A⊃(B⊃C) assumption.

Sequent Calculus- Implication Step2

And again, on our newfound B⊃C assumption.

Sequent Calculus- Implication Step3.png

Wait! By now our context by now contains A, B, and C. Each leaf of the proof tree is provable by hyp.

Sequent Calculus- Implication Step4

QED. It is instructive to compare this sequent calculus proof with the analogous natural deduction (which we solved together, last time).

Sequent Calculus- Implication Comparing Proofs

Example 2: Distributivity

Show that (A ∨ (B ∧ C)) ⊃ ((A ∨ B)  ∧ (A ∨ C)).

The first two steps here are straightforward. Simplify the conjecture string!

Sequent Calculus- Distributivity Step0 (1)

Note that Γ = { A ∨ (B ∧ C) }. Here, we use ∨L to split this assumption into two components:

Sequent Calculus- Distributivity Step1 (2)

We now have four conjectures to prove. Fortunately, each proof has become trivial:

Sequent Calculus- Distributivity StepF

QED.

Takeaways

In this post, we introduced sequent calculus (SC) as an alternative deductive calculus. Sequent calculus makes the notion of context (assumption set) explicit: which tends to make its proofs bulkier but more linear than the natural deduction (ND) style. The two approaches share several symmetries: SC right rules correspond fairly rigidly to ND introduction rules, for example.

If you want to learn sequent calculus for yourself, I recommend solving the converse problems to the two examples above. Specifically,

  • Given (A ⊃ B) ⊃ (B ⊃ C), show that A ⊃ (B ⊃ C).
  • Given (A ∨ B) ∧ (A ∨ C), show  that A ∨ (B ∧ C).

Until next time!

 

Logic Inference: Natural Deduction

kevinbinz Leave a comment

Part Of: Logic sequence
Content Summary: 500 words, 5 min read

Introduction

Logical systems like IPL have the following ingredients:

  • A proposition is an atomic statement that can acquire a truth value.
  • A connective takes atomic propositions, and melds them into a composite.

We can label propositions in the language of verification.

  • ↑ represents conjecture: propositions that require verification
  • ↓ represents knowledge: propositions that can be used for verification.

Introduction and elimination rules can be expressed in this language:

Logic Metalanguage- Original Rules (1)

Elimination rules tend to “point down”; introduction rules point up. Roughly, deduction involves applying such rules until the paths meet:

IPL Inference- Schematic

Enough theory! Let’s see how this works in practice.

Exercise One: Implication Exploration

Given A ⊃ (B ⊃ C), show that  (A ⊃ B) ⊃ (B ⊃ C).

We can visualize the challenge as follows. The red line indicates common knowledge.

IPL Inference- Implication Exploration Step0

First, let’s apply elimination on the premises:

IPL Inference- Implication Exploration Step1

Next, let’s apply introduction on the conclusion:

IPL Inference- Implication Exploration Step2.png

Are we done? No: we have not verified A↑ and B↑. If we had, they would have a red line over them.

To finish the proof, we need to invoke our introduction-rule assumptions.

IPL Inference- Implication Exploration Step3

Proving A↑ is trivial. Proving B↑ requires combining assumptions via elimination.

IPL Inference- Implication Exploration Step4 (2)

Done. 🙂 Good work!

Exercise for the Reader

Prove the converse is true. Given (A ⊃ B) ⊃ (B ⊃ C), show that A ⊃ (B ⊃ C).

Example 2: Distributivity

In arithmetic, distributivity refers to how addition and multiplication can interleave with one another. It requires that a + (b * c) = (a*b) + (a*c). For example:

  • 2 * (4+5) = 2 * 9 = 18
  • (2*4) + (2*5) = 8 + 10 = 18

Are logical conjunction and disjunction distributive? Let’s find out!

IPL Inference- Distributivity Exploration Step0 (1)

First, let’s introduce conjunction on the conclusion.

IPL Inference- Distributivity Exploration Step1

Here we reach an impasse. We need to introduce disjunction elimination on the premise. But what should we choose for C?

Let’s set C = A or B.

IPL Inference- Distributivity Exploration Step2.png

Filling in the gaps is straightforward. On the right, we eliminate conjunction and retain B. Then we introduce disjunction on both sides.

IPL Inference- Distributivity Exploration Step2 (1)

Here is where I originally got stuck. How can we use disjunction elimination?

The way forward becomes easier to grasp, when you remember:

  • We can use knowledge as many times as we like.
  • The symbols in the rule schematics are arbitrary.

Let’s set the arbitrary elimination symbol “C”  equal to A or C:

IPL Inference- Distributivity Exploration Step4 (1)

From here, the solution is straightforward.

IPL Inference- Distributivity Exploration Step5 (1)

Exercise for the Reader

Prove the converse is true. Given (A ⊃ B) ⊃ (B ⊃ C), show that A ⊃ (B ⊃ C).

Takeaways

In this post, we saw worked examples of deduction. Specifically:

  • Given A ⊃ (B ⊃ C),  show that  (A ⊃ B) ⊃ (B ⊃ C).
  • Given A ∨ (B ∧ C), show that (A ∨ B) ∧ (A ∨ C).

The best way to learn is practice. For the interested reader, I recommend these exercises:

  • Given (A ⊃ B) ⊃ (B ⊃ C), show that A ⊃ (B ⊃ C).
  • Given (A ∨ B) ∧ (A ∨ C), show  that A ∨ (B ∧ C).

In the latter exercise, you must also “get creative” on how to use disjunction elimination. Instead of choosing an arbitrary C, you must set A^B to a useful value.

… still stuck? Okay, see solution here. 🙂

Until next time.

 

Five Tribes of Machine Learning

kevinbinz 3 Comments

Part Of: Machine Learning sequence
Content Summary: 900 words, 9 min read

ML is tribal, not monolithic

Research in artificial intelligence (AI) and machine learning (ML) has been going on for decades. Indeed, the textbook Artificial Intelligence: A Modern Approach reveals a dizzying variety of learning algorithms and inference schemes. How can we make sense of all the technologies on offer?

As argued in Domingos’ book The Master Algorithm, the discipline is not monolithic. Instead, five tribes have progressed relatively independently. What are these tribes?

  1. Symbolists use formal systems. They are influenced by computer science, linguistics, and analytic philosophy.
  2. Connectionists use neural networks. They are influenced by neuroscience.
  3. Bayesians use probabilistic inference. They are influenced by statistics.
  4. Evolutionaries are interested in evolving structure. They are influenced by biology.
  5. Analogizers are interested in mapping to new situations. They are influenced by psychology.

Expert readers may better recognize these tribes by their signature technologies:

  • Symbolists use decision trees, production rule systems, and inductive logic programming.
  • Connectionists rely on deep learning technologies, including RNN, CNN, and deep reinforcement learning.
  • Bayesians use Hidden Markov Models, graphical models, and causal inference.
  • Evolutionaries use genetic algorithms, evolutionary programming, and evolutionary game theory.
  • Analogizers use k-nearest neighbor, and support vector machines.

Five Tribes- Strengths and Technologies

In fact, my blog can be meaningfully organized under this research landscape.

History of Influence

Here are some historical highlights in the development of artificial intelligence.

Symbolist highlights:

  • 1950: Alan Turing proposes the Turing Test in Computing Machinery & Intelligence.
  • 1974-80: Frame problem & combinatorial explosion caused First AI Winter.
  • 1980: Expert systems & production rules re-animate the field. 
  • 1987-93: Expert systems too fragile & expensive, causing the Second AI Winter.
  • 1997: Deep Blue defeated reigning chess world champion Gary Kasparov.

Connectionist highlights:

  • 1957: Perceptron invented by Frank Rosenblatt.
  • 1968: Minsky and Papert publish the book Perceptrons, criticizing single-layer perceptrons. This puts the entire field to sleep, until..
  • 1986: Backpropagation invented, and connectionist research restarts.
  • 2006: Hinton et al publish A fast learning algorithm for deep belief nets, which rejuvinates interest in Deep Learning.
  • 2017: AlphaGo defeats reigning Go world champion, using DRL.

Bayesian highlights:

  • 1953: Monte Carlo Markov Chain (MCMC) invented. Bayesian inference finally becomes tractable on real problems.
  • 1968: Hidden Markov Model (HMM) invented.
  • 1988: Judea Pearl authors Probabilistic Reasoning in Intelligent Systems, and creates the discipline of probabilistic graphical models (PGMs).
  • 2000: Judea Pearl authors Causality: Models, Reasoning, and Inference, and creates the discipline of causal inference on PGMs.

Evolutionary highlights

  • 1975: Holland invents genetic algorithms.

Analogizer highlights

  • 1968: k-nearest neighbor algorithm increases in popularity.
  • 1979: Douglas Hofstadter publishes Godel, Escher, Bach.
  • 1992: support vector machines (SVMs) invented.

We can summarize this information visually, by creating an AI version of the Histomap:

Five Tribes- Historical Size and Competition (2)

These data are my own impression of AI history. It would be interesting to replace it with real funding & paper volume data.

Efforts Towards Unification

Will there be more or fewer tribes, twenty years from now? And which sociological outcome is best for AI research overall?

Theory pluralism and cognitive diversity are underappreciated assets to the sciences. But scientific progress is often heralded by unification. Unification comes in two flavors:

  • Reduction: identifying isomorphisms between competing languages,
  • Generalization: creating a supertheory that yields antecedents as special cases.

Perhaps AI progress will mirror revolutions in physics, like when Maxwell unified theories of electricity and magnetism.

Symbolists, Connectionists, and Bayesians suffer from a lack of stability, generality, and creativity, respectively. But one tribe’s weakness is another tribe’s strength. This is a big reason why unification seem worthwhile.

What’s more, our tribes possesses “killer apps” that other tribes would benefit from. For example, only Bayesians are able to do causal inference. Learning causal relations in logical structure, or in neural networks, are important unsolved problems. Similarly, only Connectionists are able to explain modularity (function localization). Symbolist and Bayesian tribes are more normative than Connectionism, which makes their technologies tend towards (overly?) universal mechanisms.

Symbolic vs Subsymbolic

You’ve heard of the symbolic-subsymbolic debate? It’s about reconciling Symbolist and Connectionist interpretations of neuroscience. But some (e.g., [M01]) claim that both theories might be correct, but at different levels of abstraction. Marr [M82] once outlined a hierarchy of explanation, as follows:

  • Computational: what is the structure of the task, and viable solutions?
  • Algorithmic: what procedure should be carried out, in producing a solution?
  • Implementation: what biological mechanism in the brain performs the work?

One theory, supported by [FP98] is that Symbolist architectures (e.g., ACT-R) may be valid explanations, but somehow “carried out” by Connectionist algorithms & representations.

Five Tribes- Tribes vs Levels (2)

I have put forward my own theory, that Symbolist representations are properties of the Algorithmic Mind; whereas Connectionism is more relevant in the Autonomic Mind.

This distinction may help us make sense for why [D15] proposes Markov Logic Networks (MLN) as a bridge between Symbolist logic and Bayesian graphical models. He is seeking to generalize these technologies into a single construct; in the hopes that he can later find a reduction of MLN in the Connectionist paradigm. Time will tell.

Takeaways

Today we discussed five tribes within ML research: Symbolists, Connectionists, Bayesians, Evolutionaries, and Analogists. Each tribe has different strengths, technologies, and developmental trajectory. These categories help to parse technical disputes, and locate promising research vectors.

The most significant problem facing ML research today is, how do we unify these tribes?

References

  • [D15] Domingos (2015). The Master Algorithm
  • [M01] Marcus (2001). The Algebraic Mind
  • [M82] Marr (1982). Vision
  • [FP98] Fodor & Pylyshyn (1998). Connectionism and cognitive architecture: A critical analysis

Logic Design: Harmony in IPL

kevinbinz Leave a comment

Followup To: Logic Structure: Connectives in IPL
Part Of: Logic sequence
Content Summary: 300 words, 3 min read

Motivations

Last time, we looked at Intuitionistic Propositional Logic (IPL). In IPL, there are five connectives, and hence five introduction-elimination pairs:

IPL- All Rules (1)

What if you had to design a new logic from scratch? Suppose we were to invent five new connective symbols. Would you start by defining their introduction rule, and use these to infer elimination? Or would you instead define elimination first?

This choice reflects different ways to interpret the semantics of logic:

  • The verificationist starts with introduction first. For them, the meaning of a connective is in their constructor (introduction rules).
  • The pragmatist starts with elimination first. For them, the meaning of a proposition is how you use it.

But if introduction and elimination rules agree, then a logical system has harmony.

How do we evaluate harmony in practice? Harmony is defined as two propositions:

  • Local soundness: if I introduce and then eliminate a connective, do I gain information? If so, the elimination rule is too weak.
  • Local completeness: if I eliminate then re-introduce connective, do I lose information? If so, the elimination rule is too strong.

Demonstrating Harmony in IPL

We can show that conjunction rules exhibit harmony.

IPL Harmony- Conjunction Connective (1)

Note that we have only shown soundness for left-elimination. But demonstrating soundness for right-elimination is highly analogous.

Implication rules also exhibit harmony.

IPL Harmony- Implication Connective (4)

So does disjunction.

IPL Harmony- Disjunction Connective (5)

It is trivial to demonstrate the harmony of truth and falsity. Thus, we can say that IPL, as a formal system, has harmony.

Takeaways

In this article, we have discussed harmony, which helps us evaluate how useful a given formal system is. This notion may seem straightforward in IPL; however, it will prove useful in designing new logics, such as linear logic.

Another more subtle point to consider is that the soundness demonstration also seems to reflect a logic of simplification. This point will return when we discuss the Curry-Howard-Lambek correspondence, and the deep symmetries between logic and computation.

Until next time.

Constraint Satisfiability: Zebra Puzzle

kevinbinz 3 Comments

Part Of: Logic sequence
Content Summary: 1000 words, 10 min read.

Today, we look at the Zebra Puzzle (aka Einstein Puzzle). According to legend, Albert Einstein invented this as a child, and claimed that 98% of the human population cannot solve it.

Let’s see if we are in the 2%.

The Puzzle

Five men of different nationalities and with different jobs live in consecutive houses on a street. These houses are painted different colors. The men have different pets and have different favorite drinks. The following rules are provided:

  1. The English man lives in a red house
  2. The Spaniard owns a dog
  3. The Japanese man is a painter
  4. The Italian drinks tea
  5. The Norwegian lives in the first house on the left
  6. The green house immediately to the right of the white one
  7. The photographer breeds snails
  8. The diplomat lives in the yellow house
  9. Milk is drunk in the middle house
  10. The owner of the green house drinks coffee
  11. The Norwegian’s house is next to the blue one
  12. The violinist drinks orange juice
  13. The fox is in a house that is next to that of the physician
  14. The horse is in a house next to that of the diplomat

Who owns a zebra? And whose favorite drink is mineral water?

To answer this problem, we must learn 5 house-nation-color-drink-pet-job combinations. A solution might look like this:

  • Yellow far-left house has Norwegian diplomat who drinks water and owns a fox
  • White left house has Italian photographer who drinks tea and owns a zebra.
  • Red middle house has English photographer who drinks milk and owns snails.
  • Green right house has Spanish physician who drinks OJ and owns a dog
  • Blue far-right house has Japanese painter who drinks coffee and owns a horse.

But this solution is incorrect: it violates Rule 6: “The green house immediately to the right of the white one.”

How do we find a solution that doesn’t violate any of our constraints? Does one even exist? Or is this set of constraints not satisfiable?

Formalizing Logical Structure

Words are distracting. Let’s use symbols instead.

Einstein's Puzzle- Symbol Code (7)

With this code, we can write the above solution as a matrix.

Einstein's Puzzle- Solution Matrix

We can also formalize our constraints.

Einstein's Puzzle- Constraint Formalization

These constraints are ugly. Let’s write them in matrix form instead!

Einstein's Puzzle- Constraint Matrix Horizontal (1)

Constraint Satisfaction as a Jigsaw Puzzle

We can use the above constraints to visually check satisfiability. Whereas before you had to parse the meaning of Rule 6 verbally, now you can just inspect whether there is a visual match between rule and solution.

Einstein's Puzzle- Visual Satisfiability Check (1)

One way to determine satisfiability is to perform these checks until you find a viable solution. But this is computationally expensive: there are 25 billion solutions. Instead of inspecting every possible solutions, why don’t we generate one solution?

How? Since our Rules are used for solution-checking, why can’t we use them for solution-building?

On this view, solution building takes on the flavor of a jigsaw puzzles. Each constraint is a puzzle piece, from these ingredients we construct the solution.

sat2

Unfortunately, there is more than one way to solve a 5×5 jigsaw puzzle. Let me show you one way to solve this one. We will be use choice minimization to simplify our lives: try to play the move with the fewest degrees of freedom.

Solution: Path A

Rule 5 and 9 relate to the houses, they are easy to apply.

After these, the Rule 11 puzzle piece fits unambiguously.

sat_path0

Let’s apply Rule 6 next. That jigsaw piece can fit in two locations, the M+R columns, or the R + FR columns. Gotta choose one: let’s select the former. After that move, Rule 10 fits unambiguously.

The FR column is the only place that has an unclaimed nation and color: Rule 1 must go there. similarly, the FL column is the only available spot for Rule 8.

sat_patha1

Here we can apply Rule 14 (the original clue’s wording “The horse is in a house next to that of the diplomat” means that the puzzle piece can be flipped horizontally).

After that, only column L can accommodate Rule 4. Then FR must accept Rule 12. 

sat_patha2

Disaster! Consider Clue 2, 3, and 7. These rules are mutually exclusive (they have at least one row in common with one another), and have overlapping domains (they all cannot fit in FL, but must fit in either M or R).

Einstein's Puzzle- hPath A3 Paradox

This is the pigeonhole principle: just as three pigeons cannot fit into two holes, there is no way to reach a solution.

Does that mean the puzzle is unsolvable? No, it means we explore other choices.

Solution: Path B

Let’s return to the other possible placement of Rule 6. Instead of putting it in M+R columns, we’ll put it in R+FR. Then, Rules 10, 1, 8, and 14 follow inevitably (each has precisely one choice).

sat_pathb1

Here we face another choice: do we put puzzle piece 4 in the left or right house? Let’s choose the right house. Then, Rule 12 and Rule 3 follow logically.

sat_pathb2

Alas! Another disaster. Rule 2 doesn’t fit. 😦

Solution: Path C

Retrace our steps! The last choice we made was Place(4, R). What if we place it in the left house instead?

sat_pathc1

To our delight, we now see that Path 2b is the only correct logical journey through our puzzle.  The concluding steps are given below, and the desired quantities are shown in the “missing” tiles.

sat_pathc2

Recall the original questions:

Who owns a zebra (P5)? Whose favorite drink is mineral water (D5)?

Our symbol table can translate our answer:

The Japanese man (N3) owns the zebra, and the Norwegian (N5) drinks mineral water

Implications

The above solution is nothing more to solving a 5×5 jigsaw puzzle. I suspect this technique will only become clear with practice. Go solve Einstein’s Riddle on your own, or one of these variants!

For the solution above, it is helpful to review our search history. Remarkably, we only faced two choices in our solution. When one branch failed, we turned out attention to other branches. This is known as recursion, and will be the subject of another blog post.

Einstein's Puzzle- Search History (2)

Many programming solutions exist for these kinds of problems. In practice, libraries can be used to write more concise solvers.

This kind of problem is called propositional satisfiability (SAT), or constraint programming (CP), although these two disciplines differ in subtle ways.

As we will see next time, SAT problems are at the root of complexity theory and artificial intelligence. Until then.

Complementary Learning Systems

kevinbinz Leave a comment

Part Of: Demystifying Memory sequence
Content Summary: 1000 words, 10 min read

1.

Your brain is constantly keeping track of the world and your body. It represents these ever-changing environments by patterns of neural activation. Knowledge is not kept in the neurons themselves, but in the connections between neurons.

Sometimes, the brain will discover useful regularities in the environment, and store these patterns for later use. This is long-term memory. We shall concern ourselves with five kinds of long-term memory:

  1. Episodic: ability to remember events or episodes (e.g., dinner last Tuesday night)
  2. Semantic: ability to remember facts and concepts (e.g., hands have five fingers)
  3. Procedural: ability to develop skills (e.g., playing the piano).
  4. Behavioral: ability to remember stimulus-outcome pairs (e.g., bell means food)
  5. Emotional: ability to remember emotional information (e.g., she is always angry).

These memory systems are computed in different areas of the brain.

  1. Episodic memories are computed by the hippocampus
  2. Semantic memories are computed by the association neocortex
  3. Procedural memories are computed by the somatosensory neocortex
  4. Behavioral memories are computed by the basal ganglia
  5. Emotional memories are computed by the central amygdala

Only episodic and semantic memory are directly accessible to consciousness (i.e., working memory). The others are just available to the autonomous mind.

CLS- Categories of Long-Term Memory (1)

2.

We have previously described conscious experience as a mental movie. But, unlike a normal theater, consciousness has several screens, each of which playing a different sense modality. visual, audio information etc. Call this the multimodal movie.

Semantic memory come in two forms: encyclopedic memory (abstract descriptions of events) and conceptual memory (concepts and their inter-relationships). Both abstractions are derived from the movie, by removing redundant information.

CLS- Episodic vs Semantic Memory

Mind wandering is the tendency of animals to recall past experiences. But why does mind wandering resurrect the details of what was seen, heard, smelled, touched? Why not simply use the plot summary (encyclopedic memory) instead?

Why does episodic memory exist at all?

3.

Henry Molaison was born on February 26, 1926. As a child, he suffered from epilepsy.

CLS- Patient HM (2)

His doctors removed what they thought to be the source of the seizures: the hippocampus. After the surgery, Henry still recognized objects, was able to solve puzzles, even had the same IQ. He had a rich emotional life, and could learn new skills (e.g., to play the piano). But he was completely incapable of forming new episodic memories. Henry (i.e., Patient HM) was locked in a 5 minute loop, never remembering prior events.

Let’s imagine different kinds of amnesia Henry might have experienced.

Scenario 1. Henry has no retrograde amnesia (old memories were unperturbed), but suffers severe anterograde amnesia (unable to create new memories). From this data, we might conclude that the hippocampus creates, but does not store, episodic memories.

CLS- HM Amnesia Pattern v1 (1)

Scenario 2. Henry experiences both severe retrograde and anterograde amnesia. From this data, we might conclude that the hippocampus creates and stores episodic memories.

CLS- HM Amnesia Pattern v2 (2)

Neither scenario actually happened. Instead, Henry experienced temporally graded retrograde amnesia:

CLS- HM Amnesia Pattern v3 (2)

This shows that, while the hippocampus creates and stores episodic memories, these memories are eventually copied elsewhere. This process is called consolidation. Hippocampal damage destroy memories that have not yet been consolidated. 

But why should the brain copy memories? This seems inefficient. And why does this process take years, even decades?

4.

The connectionist paradigm models the brain as a neural network. The AB-AC task illustrates a challenge for connectionism. It goes as follows:

You want to associate stimulus A with response B. For example, when you hear “chair”, you should say “map”. There are many such associations (Chair-Map, Book-Dog, Car-Idea). This is the AB list.

After you achieve 100% recall on the AB list , a new set of stimulus-response words are given: the AC list. You want to learn both. However, the AB and AC lists have the same stimuli paired with novel responses (e.g. Chair-Printer, Book-Flower, Car-Shirt).

How well do humans and connectionist models do against this task? Let’s find out! The following graphs take place after the AB list has been learned perfectly. Y-axis is %correct, x-axis is number of exposures to the AC list.

CLS- Catastrophic Interference (2)

Consider the left graph. Dotted line is AC recall over time. Humans were able to learn the AC list. The solid line shows AB list performance. As humans learned AC associations, their AB performance suffered a little, from 100 to 60%. This is moderate interference.

Consider the right graph. Dotted line shows that the model is able to learn the AC list, just like the human. But solid line shows that AB recall very quickly drops to 0%. This is catastrophic interference.

Catastrophic interference occurs when the AB list and AC list are learned separately (focused learning). But what if you learn them at the same time? More specifically, what if you train against a shuffled set of AB and AC associations (interleaved learning)?

CLS- Interleaved vs Focused Learning (2)

On the left, focused learning (black squares) shows catastrophic interference against AB memories, as before. But interleaved learning (white dots) show zero interference!

On the right, we see another consequence of interleaved learning: new memories are acquired much more slowly.

5.

We are ready to put the puzzle together.

Catastrophic interference is an inevitable consequence of systems that employ highly-overlapping distributed representations, despite the fact that such systems have a number of highly desirable properties (e.g., the ability to perform generalization and inference).

This problem can be addressed by employing a structurally distinct system with complementary learning properties: sparse, non-overlapping representations that are highly robust to interference from subsequent learning. Such a sparse system by itself would be like an autistic savant: good at memorization but unable to perform everyday inferences. But when paired with the highly overlapping system, a much more versatile overall system can be achieved.

The neocortex and hippocampus comprise these learning systems:

CLS- Two Component Model

First introduced in 1995, Complementary Learning System (CLS) theory predicts a wide range of extant biological, neuropsychological, and behavioral data. It explains why the hippocampus exists, why it performs consolidation, and why consolidation takes years to complete.

The CLS theory was first presented in [M95]. Data in section 4 taken from that paper. Section 5 quotes liberally from [O11].

  • [M95] McClelland et al (1995). Why There Are Complementary Learning Systems in the Hippocampus and Neocortex: Insights From the Successes and Failures of Connectionist Models of Learning and Memory
  • [O11] O’Reilly et al (2011). Complementary Learning Systems