Author kevinbinz

[Sequence] Algebra

kevinbinz Leave a comment

Logic

Set Theory

Abstract Algebra

Linear Algebra

Category Theory

Related sequences

An Introduction to Linear Algebra

kevinbinz Leave a comment

Part Of: Algebra sequence
Content Summary: 1300 words, 13 min read.

Linear algebra is the math of vectors and matrices. Let me attempt to explain it as succinctly as possible.

Vector Operations

If n is a positive integer and ℝ is the set of real numbers, then ℝn is the set of all n-tuples of real numbers.  A vector v ∈ ℝn is one such n-tuple. For example,

V = (v_1, v_2, v_3) \in (\mathbb{R}, \mathbb{R}, \mathbb{R}) \equiv \mathbb{R}^3

The six vector operations are: addition, subtraction, scaling, cross product, dot product, norm (vector length). For vectors u and v, these are defined as follows:

linear-algebra-vector-operations-1

The dot product and the cross product norm are related to the angle between two vectors. Specifically,

u \cdotp v = \|u\| \|v\| cos(\theta)

\|u \times v\| = \|u\| \|v\| sin(\theta)

Finally, note the the cross product is not commutative: u x v != v x u.

Matrix Operations

A matrix A ∈ ℝm x n is a rectangular array of real numbers with m rows and n columns. For example,

A= \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{bmatrix} \in \begin{bmatrix} \mathbb{R} & \mathbb{R} \\ \mathbb{R} & \mathbb{R} \\ \mathbb{R} & \mathbb{R} \\ \end{bmatrix} \equiv \mathbb{R}^{3x2}

Important matrix operations are addition, subtraction, product, transpose, and determinant:

linear-algebra-matrix-operations-2

Of the above operations, matrix product is especially significant. This operation is only possible when A has the same number of columns as B has rows.

Matrix as Morphism

Importantly, matrices with one row or one column can interpreted as vectors. Matrix multiplication with a vector can be interpreted in two ways. The row picture interprets the output as a dot product, the column picture interprets the output as a linear combination.

linear-algebra-row-vs-column-picture-4

Let’s take A to be a 2 by 2 matrix with row-vectors (2, -1) and (-1,2), and let b = (0,3). When we solve for x, we find there are two ways to do so:

linear-algebra-row-vs-column-geometry-1

In the above example, we set b = (0,3). But this linear combination could generate any vector b. In general, linear combinations can generate the entirety of a space (in this case, a two-dimensional plane). 

In both views, we say A transform x → b. If vectors are groups of data, matrices are functions that operate on vectors. Specifically, multiplication by a matrix A ∈ ℝm x n we will call a linear transformation, that converts an n-tuple into a m-tuple TA : ℝn → ℝm.

The symmetry between functions and linear transformations runs deep. When we explore category theory, we will discover the structure underpinning this relationship. But in the meantime, consider the following equivalences:

linear-algebra-function-vs-linear-transformation-4

Especially important to matrix functions is the notion of inverse matrix. Just as f-1(x) = ln(x) undoes the effects of f(x) = ex, inverse matrix A-1 undoes the effects of A. The cumulative effect of applying A-1 after A is the identity matrix A-1A = 1. The identity matrix is analogous to multiplying by one, or adding zero: it is algebraically inert.

Only square matrices can be invertible, because reversal is commutative AA-1 = A-1A = 1. But not all square matrices have inverses. The determinant of a matrix checks for invertibility. Det(A) != 0 iff A is invertible.

Matrix inversion is vitally important to solving systems of linear equations.

  • AX = B → multiply both sides by A-1 on the right → X = A-1B
  • XA = B → multiply both sides by A-1 on the right → X = BA-1
  • ABXC = E → put C-1 on the right and B-1A-1 on the left → X = B-1A-1EC-1

Elimination As Inverse Solver

To solve Ax = b, we must find inverse matrix A-1. This can be done via Gauss-Jordan Elimination. This method affords three row operations:

  1. Linear Combination: Ri += kRj
  2. Scaling: Ri *= k
  3. Row Swap: Ri ⇆ Rj

After creating a matrix of the form Ax = b, we can solve for x by creating an augmented matrix of the form [ A | b ], and converting the left-hand side into the identity matrix:

linear-algebra-gauss-jordan-elimination-2

To solve for x algebraically, Ax = b → A-1Ax = A-1b → 𝟙x = A-1b. So Gauss-Jordan facilitates the discovery of inverse matrix A-1. We can show this computation explicitly, by setting an augmented matrix of form [ A | 1 ]

linear-algebra-gauss-jordan-inverse-matrix-6

Row operations are functions that act on vectors. So are matrices. Thus, it isn’t very surprising that our three row operations each correspond to an elementary matrix. The elementary matrix is similar to the identity matrix; in the below picture, only the shaded region diverges. 

linear-algebra-elementary-matrices-7

We now see that the row operations of Gauss Jordan elimination are a kind of factoring: we are finding the elementary matrices underlying A-1:

linear-algebra-gauss-jordan-elementary-matrices-2

Thus E4E3E2E1 = A-1 and Ax = b → (E4E3E2E1)Ax = (E4E3E2E1)b → x = A-1b

Fundamental Vector Spaces

A vector space consists of a set of vectors and all linear combinations of these vectors. The set of all linear combinations is called the span. For example, the vector space S = span{ v1, v2 } consists of all vectors of the form v = ɑv1 + βv2, where ɑ and β are real numbers.

Vector spaces can be characterized by a basis: the original set of vectors whose linear combination creates the vector space. The vectors of any basis must be linearly independent, or orthogonal. You can check whether two vectors or orthogonal by confirming their dot product u · v = 0. The dimension of a vector space is the cardinality of the basis (number of orthogonal vectors).

Recall that matrices are functions that project vectors from ℝn to ℝm. This corresponds to projecting from row space to column space, as follows:

linear-algebra-fundamental-space-interpretation-6

We will unpack the full implications of this graphic another time. For now, it suffices to understand that discovering the bases of these subspaces is a useful exercise.

For example, if we show that a matrix has an non-empty kernel, this in itself is proof of non-invertibility. Why? Because if TA sends a vector to the zero vector, there is no TA-1 that can undo this operation.

We can say more. For an n x n matrix A, the following statements are equivalent:

  1. A is invertible
  2. The determinant of A is nonzero.
  3. The RREF of A is the n x n identity matrix
  4. The rank of the matrix is n
  5. The row space of A is ℝn
  6. The column space of A is ℝn
  7. A doesn’t have a null space (only the zero vector N(A) = {0} )

Elimination as Basis Identifier

We have seen elimination discover (and factorize) the matrix inverse. But what happens when an inverse does not exist? Well, elimination has a natural, unique stopping point:

linear-algebra-rref-derivation-2

Matrices in reduced row echelon form (RREF) have the following properties:

  1. Rows with all zeroes are moved to the bottom.
  2. The first nonzero number from the left (pivot) is to the right of the pivot above it.
  3. Every pivot equals 1 and is the only nonzero entry in its column

Gauss-Jordan Elimination can replace every matrix with an equivalent one in rref form. Note that we have seen several examples of elimination creates the identity matrix 1  when A is invertible. This is only possible because 1 fits the rref criteria.

Once a matrix is in rref form, it becomes trivial to discover the basis for its three fundamental spaces:

  • R(A) basis: all row vectors that are non-zero
  • C(A) basis: all column vectors that contain pivot.
  • N(A) basis: the solution to Ax = 0

linear-algebra-deriving-fundamental-spaces-2

We see that rank(A) + nullity(A) = 3 + 1 = 4, which indeed is the number of columns. Also, the column space of A equals the row space of AT. This is not an accident, since transpose simply swaps rows with columns.

Takeaways

  • Vectors are groups of numbers; matrices are functions that act on vectors.
  • We can solve linear equations by conducting Gauss-Jordan elimination.
  • Gauss-Jordan elimination-based solution rely on searching for inverse matrix A-1
  • The domain of matrices is its row vectors, its codomain is its column vectors.
  • Even if a matrix is not invertible, elimination can find its most reduced form (RREF).
  • RREF matrices can be used to derive fundamental subspaces.

Until next time.

Related Works

Algorithmic Dark Matter: Duality in Linear Programming

kevinbinz Leave a comment

Part Of: Optimization sequence
Content Summary: 800 words, 8 min read.

Today, I introduce the concept of duality. Buckle your seat belts! 🙂

Max Flow algorithm

The problem of flow was originally studied in the context of the USSR railway system in the 1930s. The Russian mathematician A.N. Tolstoy published his Methods of finding the minimal total kilometrage in cargo-transportation planning in space, where he formalized the problem as follows.

We interpret transportation graphically. Vertices are interpreted as cities, and edges are railroads connecting two cities. The capacity of each edge was the amount of goods that particular railroad could transport in a given day. The bottleneck is solely the capacities, and not production and consumption. We assume no available storage at the intermediate cities.

The flow allocation problem defines source and termination vertices, s and t. We desire to maximize volume of goods transported s → t. To do this, we label each edge with the amount of goods we intend to ship on that railroad. This quantity, which we will call flow, must respect the following properties:

  • Flow cannot exceed the capacity of the railroad.
  • Flow is conserved: stuff leaving a city must equal the amount of stuff arriving.

Here are two possible solutions to flow allocation:

duality-two-flow-solutions-1

Solution B improves on A by pushing volume onto the b → c railway. But are there better solutions?

To answer rigorously, we formalize max flow as a linear optimization problem:

duality-max-flow-as-linear-optimization-1

The solution to LP tells us that no, eight is the maximum possible flow.

Min Cut algorithm

Consider another, seemingly unrelated, problem we might wish to solve: separability. Let X ⊂ E represent the number of edges you need to remove to eliminate a connection s → t. Here are two such solutions:

Duality- Two Cut Solutions (1).png

Can we do better than B? The answer is no: { (b,t), (c,d) } is the minimum cut possible in the current graph. In linear programming terms, it is the Best Feasible Solution (BFS)

Note that the BFS of minimum cut and the BFS of max flow arrive at the same value. 8 = 8. This is not a coincidence. In fact, these problems are intimately related to one another. What the min cut algorithm is searching for is the bottleneck: the smallest section of the “pipe” from s → t. For complex graphs like this, it is not trivial to derive this answer visually; but the separability algorithm does the work for us.

The deep symmetry between max flow and min cut demonstrates an important mathematical fact. All algorithms come in pairs. For this example, we will call max flow and min cut the primal and dual problems, respectively. We will explore the ramifications for this another time. For now, let’s approach duality from an algebraic perspective.

Finding LP Upper Bound

Consider a linear program with the following objective function:

\max (2x_1 + x_2)

And these constraints

4x_1 + x_2 \leq 6

x_1 + 2x_2 \leq 5

x_1, x_2 \geq 0

This program wants to find the largest solution possible given constraints. Can we provide an upper bound on the solution?

Yes. We can immediately say that the solution is no greater than 6. Why? The objective function, 2x_1 + x_2 is always smaller than 4x_1 + x_2, because we know all variables are positive. So we have an upper bound OPT ≤ 6. We can sharpen this upper bound, by comparing the objective function to other linear combinations of the constraints.  

duality-generalizing-search-for-upper-bounds-4

Different weights to our linear combinations produce different upper bounds:

  • (1,0) → 6
  • (0,1) → 5
  • (⅓, ⅓ ) → 3.67

Let us call these two weights (y_1, y_2). What values of these variables give us the smallest upper bound? Importantly, this is itself an objective function: \min (6y_1 + 5y_2).

But y_1 and y_2 are constrained: they must produce an equation that exceeds 2x_1 + x_2. Thus,

y_1(a) + y_2(b) \geq 2x_1 + x_2

y_1 \left( 4x_1 + x_2 \right) + y_2 \left( 3x_1 + 2x_2 \right) \geq 2x_1 + x_2

\left(4y_1 + 3y_2 \right) x_1 + \left (y_1 + 2y_2 \right) x_2 \geq 2x_1 + x_2

(4y_1 + 3y_2) \geq 2 and (y_1 + 2y_2) \geq 1

This gives us our two constraints. Thus, by looking for the lowest upper bound on our primal LP, we have derived our dual LP:

duality-primal-vs-dual-example-4

Note the extraordinary symmetry between primal and dual LPs. The purple & orange values are mirror images of one another. Further, the constraint coefficient matrix has transposed (the 3 has swapped along the diagonal). This symmetry is reflected in the above linear algebra formulae. 

A Theory of Duality

Recall that linear programs have three possible outcomes: infeasible (no solution exists), unbounded (solution exists at +/-∞) or feasible/optimal. Since constraints are nothing more than geometric half-spaces, these possible outcomes reflect three kinds of polyhedra:

duality-three-possible-outcomes

The outcome of primal and dual programs are predictably correlated. Of the nine potential pairings, only four can actually occur:

  1. Both P and D are infeasible
  2. P is unbounded and D is infeasible
  3. D is unbounded and P is infeasible
  4. Both are feasible, and there exist optimal solutions

Finally, in the above examples, we saw that the optimal dual value p^* = d^* (8=8). But this is not always the case. In fact, the optimal dual value can be smaller .

We can distinguish between two kinds of duality:

  • Strong duality, where p^* = d^*
  • Weak duality, where p^* - d^* \geq 0

Takeaways

Today, we have illustrated a deep mathematical fact: all problems come in pairs. Next time, we will explore the profound ramifications of this duality principle.

Related Resources: CMU Lecture 5: LP Duality

An Introduction to Probability Theory

kevinbinz Leave a comment

Part Of: Statistics sequence
Related To: An Introduction to Set Theory
Content Summary: 400 words, 4 min read.

“Probability theory is nothing but common sense reduced to calculation.” – Laplace

Introducing Probability Theory

Probability theory, as formulated by Andrey Kolmogorov in 1925, has two ingredients:

  1. A space which define the mathematical objects (“the nouns”)
  2. Axioms which define the mathematical operations (“the verbs”)

A probability space is a 3-tuple (Ω,𝓕,P):

  1. Sample Space (Ω): A set of possible outcomes, from one or more events. Outcomes in Ω must be mutually exclusive and collectively exhaustive.
  2. σ-Algebra (𝓕). A collection of event groupings, or subsets. If Ω is countable, this can simply be the power set, otherwise a Borel algebra is often used.
  3. Probability Measure Function (P). A real-valued function P: Ω → ℝ which maps from events to real numbers.

The Kolmogorov axioms provide “rules of behavior” for the residents of probability space:

  1. Non-negativity: probabilities can never be negative, P(x) >= 0.
  2. Unitarity: the sum of all probabilities is 1.0 (“something has to happen”)
  3. Sigma Additivity: the probability of composite events equals the sum of their individual probabilities.

probability-structural-overview-3

Random Variables

A random variable is a real-valued function X: Ω → ℝ. A random variable is a function, but not a probability function. Rather, instantiating random variables X = x defines a subset of events ⍵ ∈ Ω such that X(⍵) = x. Thus x picks out the preimage of Ω. Variable instantiation thus provides a language to select groups of events from Ω.

Random variables with discrete outcomes (countably finite Ω) are known as discrete random variable. We can define probability mass functions (PMFs) such that

f_X(x) = P(X=x) = P( { \omega \in \Omega : X(\omega) = x } )

In contrast, continuous random variables have continuous outcomes (uncountable Ω). For this class of variable, the probability of any particular event is undefined. Instead, we must define probabilities against a particular interval. The probability of 5.0000000… inches of snow is 0%; it is more meaningful to discuss the probability of 5 ± 0.5 inches of snowfall. Thus, we define probability density functions (PDFs) such that:

P[a \leq X \leq b] = \int f_X(x) dx

We can summarize discrete PMFs and continuous PDFs in the following graphic:

probability-pmf-vs-pdf-1

Marginal Probabilities

Consider two random variables, A and B ∈ Ω. Several operators may act on these variables, which parallel similar devices in Boolean algebra and set theory.

probability-operators

Suppose we want to know the probability of either A or B occurring. For this, we rely on the Set Combination Theorem:

probability-set-combination-4

Union involves subtracting the intersection; else the purple region is counted twice. In our post on set theory, we saw this same idea expressed as the inclusion-exclusion principle (Definition 13).

Summary

This first post in a two part explored the first six concepts or probability theory. Next time, we will learn about concepts 7-12.

probability-theory-theorems-4

These definitions and theorems are the cornerstone upon which much reasoning are built. It pays to learn them well.

Related Work

Error Correcting Codes

kevinbinz Leave a comment

Part Of: Information Theory sequence
Followup To: An Introduction To Communication
Content Summary: 900 words, 9 min read

Motivations

Information theory was first conceived as a theory of communication. An employee of Bell Labs, Shannon was interested in the problem of noise. Physical imperfections on your data cable, for example, can distort your signal. 

communication-general-architecture

How to protect against noise? One answer is to purchase better equipment.

But there is another, less expensive answer. Errors can be reduced by introducing redundancy into their signals. But redundancy has a price: it also slows the rate of communication.

Shannon strove to understand this error vs rate trade-off quantitatively. Is error-free communication possible? And if so, how many extra bits would that require?

Before we can appreciate Shannon’s solution, it helps to understand the basics of error correcting codes (ECC). We turn first to a simple ECC: replication codes.

Replication Codes

Error correcting codes have two phases: encoding (where redundancy is injected) and decoding (where redundancy is used to correct errors)

Consider repetition code R3, with the following encoding scheme:

0 → 000
1 → 111

Decoding occurs via majority rule. If most bits are zero the original bit is a 0, and vice versa. Explicitly:

000, 001, 010, 100 → 0
111, 110, 101, 011 → 1

Suppose I want to communicate the word “red” to you. To do this, I encode each letter into ASCII and send those bits over the Internet, to be consumed by your Internet browser. Using our simplified ASCII: ‘r’ → 10010. To protect from noise, we repeat each bit three times: 10010 → 111000000111000.

Let us imagine that 6 bits are flipped: 101000110001100. The last error caused the code 000 → 100, which the decoding algorithm successfully ignores. But the first two noise events caused 111 → 010, which causes a decoding error. These decoding errors in turn change the ASCII interpretation. This pattern of noise will cause you to receive the word “fed”, even though I typed “red”.

ecc-replication-code-lifecycle

Analysis of Repetition Codes

Let us formalize the majority rule algorithm. Decoding involves counting the number of bit flips required to restore the original message. We express this number as the Hamming distance. This can be visualized graphically, with each bit corresponding to a dimension. On this approach, majority rule becomes a nearest neighbor search.

hamming_distance

What is the performance of R3? Let us call noise probability p, the chance of any one bit flip. We can model the total number of errors with the binomial distribution:

ecc-binomial-distribution

In R3, a decoding error requires two bit flips within a 3-bit block. Thus, P(error) = P(r >= 2|p, 3). We can then compute the frequency of decoding errors.

ecc-replication-error-rate-analysis

For p = 10% error rate, we can graph R3 vs R5 performance:

ecc-rate-vs-error-diagram-2

Hamming Codes

In error correcting codes, we distinguish redundant bits versus message bits. Replication codes have a very straightforward mapping between these populations. However, we might envision schemes where each redundant bit safeguards multiple message bits.

Consider the Hamming code, invented in 1950. Richard Hamming shared an office with Claude Shannon for several years. He is also the father of Hamming distance metric, discussed above.

Hamming codes split messages into blocks, and add redundant bits that map to the entire block. We will be examining the H(7,4) code. This code takes 4-bit blocks, and adds three redundant bits at the end. Each redundant bit then “maps to” three of the message bits:

ecc-repetition-vs-hamming-5

We now define the encoding and decoding algorithms for Hamming Codes. Let message bits s ∈ S be organized into blocks. Let each redundant bit t ∈ T map to a particular subset of the block. For example, s(t7) → { s3, s4, s1 }.

For H(7,4) code, each redundant bit maps to a set of three message bits. If there are an odd number of 1s in this set, the redundant bit is set to 1. Otherwise, it is set to zero. Binary addition (eg., 1+1=0) allows us to express this algebraically:

ti = ∑ s(ti)

A Venn diagram helps to visualize this encoding:ecc-hamming-code-encoding-1

H(7,4) decoding is complicated by the fact that both message bits and redundant bits can be corrupted by noise. We begin by identifying whether there are any inequalities between ti versus ∑ s(ti). If there is, that means *something* has gone wrong.

For H(7,4), there are three redundant bits in every block; there are thus eight different syndromes (error signatures). The decoding algorithm must respond to each possible syndrome, as follows:

ecc-hamming-code-decoding-1

The error rate for H(7,4) is calculated as follows. 

ECC- Rate vs Error Repetition and Hamming (1).png

Application To Information Theory

This example demonstrates that Hamming codes can outperform replication codes. By making the structure of the redundant bits more complex, it is possible to reduce noise while saving space.

Can error-correcting codes be improved infinitely? Or are there limits to code performance, besides human imagination? 

Shannon proved that there are limits to error-correcting codes. Specifically, he divides the error-rate space into attainable and unattainable regions:

ecc-rate-vs-error-unattainable-region

Another important result of information theory is the design of decoding algorithms. Decoding H(7,4) is perhaps the most complex algorithm presented above. For more sophisticated ECCs, these decoding tasks become even more difficult.

Information theory provides a principled way to automate the discovery of optimal decoding algorithms. By applying the principle of maximum entropy, we can radically simplify the process of designing error-correcting codes.

We will explore these ideas in more detail next time. Until then!

Codes and Communication

kevinbinz Leave a comment

Part Of: Information Theory sequence
Content Summary: 1000 words, 10 min read

History of Communication Systems

Arguably, three pillars of modernity are: industrialization, democratic government, and communication technology. Today, we examine the latter.

Before 1860, long-distance communication required travel. This made communication across large nations quite challenging. Consider, for example, the continental United States. In 1841, it took four months for the news of the death of President Harrison to reach Los Angeles.

The Pony Express (a mail service built on horsepower) improved wait times to ten days. But it was the telegraph that changed the game. The key idea was to send messages on paper, but rather through voltage spikes in electric cables. Electrical pulses travel at near the speed of light.

In 1861, the first transcontinental cable was complete, and instantaneous communication became possible. The Pony Express closed its doors two days later.

It is hard to understate the impact of this technology. These advances greatly promoted information sharing, economic development, and improved governance.

By 1891, thousands of miles of cable had been lain underwater. These pipelines have only become more numerous and powerful over the years. Without them, the Internet would simply be impossible.

communication-undersea-pipelines

Today, we strive to understand the maths of communication. 

Understanding Communication

We start with the basics.

What is communication? The transmission of linguistic information.  

What is language? A shared system of reference communicated through symbols.

References (e.g., words) are functions that maps itself to an aspect of the physical world. References can denote both objects and actions.

Consider the power set of symbols (all possible combinations of letters). Words represent a subset of this object (a family of sets over an alphabet).

Symbol recognition is medium independent. For example, a word can be expressed either through writing (graphemes) or spoken language (phonemes).

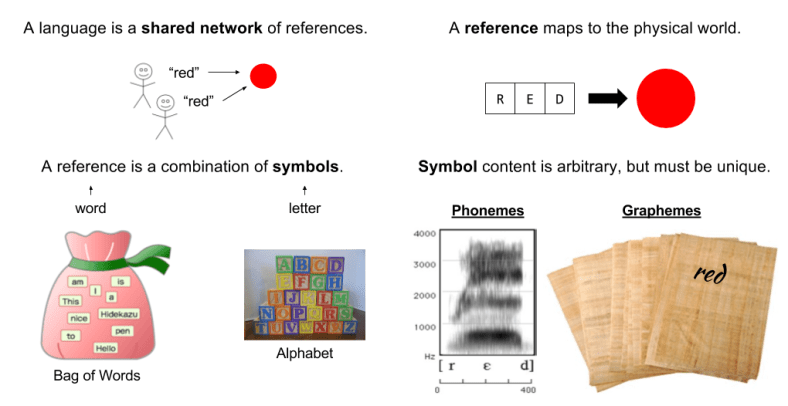
communication-language-overview-1

References are the basis of memory. They together build representations of the physical world.

All complex nervous systems construct references. Some animals can communicate (share references). Only humans do so robustly, via syntax.

Semantic interpretations are not restricted to biology. Computers can refer as well. Reference is made possible by symbol grounding.

As the substrate of reference, symbols are the basis of computation. All answerable questions can be solved by a Turing machine.

Semantic aspects of communication are irrelevant to the engineering problem. Coding theory studies symbol sets (alphabets) directly.

Comparing Alphabets

How to compare languages? Let’s find out!

There are 26 symbols in the English alphabet. How many possible three-letter words are there? The answer is 26^3 = 17,576 possible words. More generally:

Possible Messages (M) = Alphabet Size (a) ^ Number of Symbols (X)

M = aX

Log(M) = Loga(X)

Information is the selection of specific words (“red”) from the space of possible words.

We might be tempted to associate information with W. But we desire information to scale linearly with length. Two books should contain twice as much information as one. So we say information is log(M).

I(X, a) = Loga(X)

Alphabet size (logarithmic base) is not very important in this function. Suppose we choose some other base B instead. We can compare alphabets by converting logarithmic base.

Base Conversion: Logb(X) = Loga(X) / Loga(b)

I(X, a) = Loga(X) = Logb(a) * Logb(X)

I(X) = K Logb(X) where K equals Logb(a)

I(X) is known as Shannon information.

We can compare the expressive power of different alphabets. The modern Hawaiian alphabet, for example, has 13 letters. So there are only 13^3 = 2,197 possible three-letter Hawaiian words. The information provided by these respective languages is:

I(Xhawaiian) = Log13(X)

I(Xenglish) = Log13(26) * Log13(X)

I(Xenglish) / I(Xhawaiian) = Log13(26) = 1.270238

We expect English words to be 27% more information than Hawaiian, on average. And indeed, this is precisely what we find:

With 3 English letters: 26^3 = 17,576 possible words
With 3.81 Hawaiian letters: 13^(3*1.270238) = 17,576 possible words

Translating Between Codes

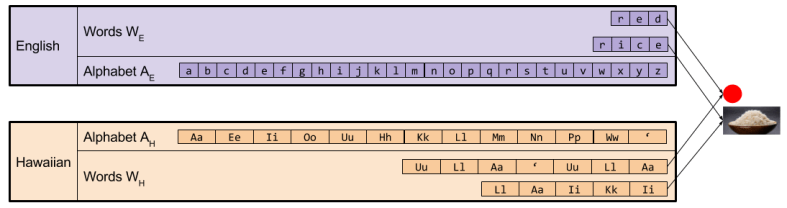
How does one translate between languages? Consider the word “red”. In Hawaiian, this word is “ula’ula”. We might construct the following function:

  • r → ula’
  • e → ul
  • d → a

But this fails to generalize. The Hawaiian word for rice is “laiki”, which does not begin with a ‘u’.

In general, for natural languages any function f: AE → AH is impossible. Why? Because words (references) map to physical reality in arbitrary ways. Two natural languages are too semantically constrained to afford a simple alphabet-based translation.

communication-translation-and-semantic-constraint

Alphabet-based translations are possible, however, if you use a thin language. Thin languages only refer when converted back into its host language. Binary is a classic example of a thin language. It has the smallest possible alphabet (size two).

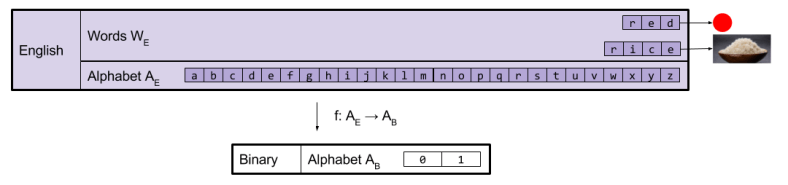
communication-thin-languages

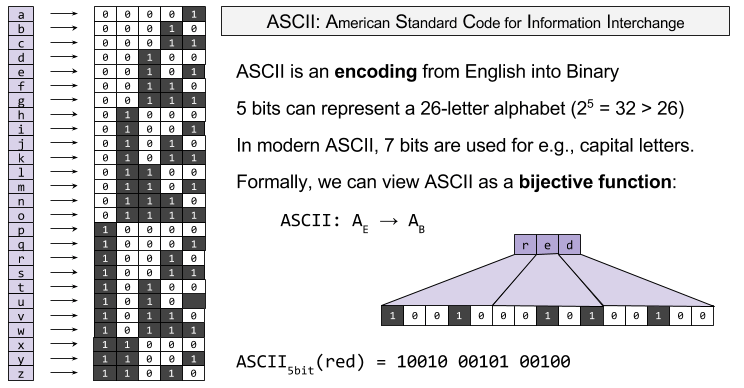
An encoding is a function of type f: AE → AH. For an example, consider ASCII. This simple encoding is at the root of most modern technologies (including UTF-8, which you are using to view this webpage):

communication-ascii-example

Noise and Discriminability

A communication system has five components: source, transmitter, channel, receiver, and destination.

A source and destination typically share a common system of reference. Imagine two people with the same interpretation of the word “red”, or two computers with the same interpretation of the instruction “lb” (load byte).

Transmitter and receiver also tend to play reciprocal roles. Information is exchanged through the channel (e.g., sound waves, cable).

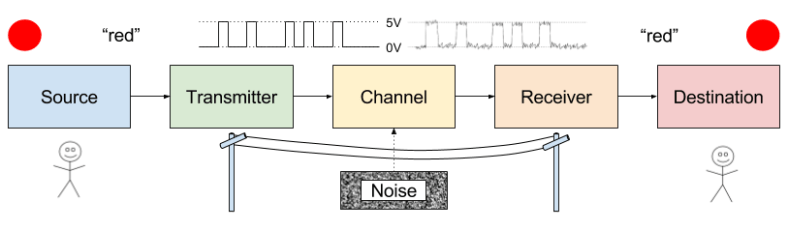
communication-general-communication-architecture

Receivers reconstruct symbols from the physical medium. Noise causes decoding errors.

How can the transmitter protect the message from error? By maximizing the physical differences between symbols. This is the discriminability principle.

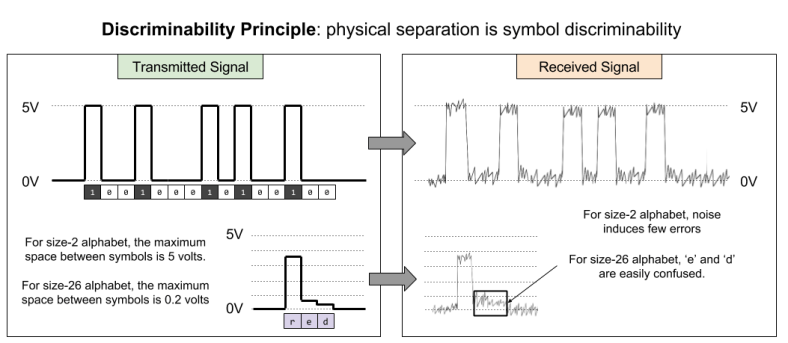
Communication- Discriminability (1).png

This principle explains why binary is employed by computers and telecommunications. A smaller alphabet improves symbol discriminability, which combats the effect of noise.

Takeaways

  • Language is a shared system of reference communicated through symbols 
  • References are functions that maps itself to an aspect of the physical world. 
  • Symbol recognition is medium independent. 
  • Alphabet size determines expressive power (how many messages are possible)
  • An encoding lets you alter (often reduce) language’s alphabet.
  • Such encodings are often desirable because they protect messages from noise.

Entropy as Belief Uncertainty

kevinbinz Leave a comment

Part Of: Information Theory sequence
Content Summary: 900 words, 9 min read

Motivations

What do probabilities mean?

A frequentist believes that they represent frequencies. P(snow) =10% means that on 100 days just like this one, 10 of them will have snow.

A Bayesian, on the other hand, views probability as degree of belief. P(snow) = 10% means that you believe there is a 10% chance it will snow today.

This subjective approach views reasoning as probability (degree of belief) spread over possibility. On this view, Bayes Theorem provides a complete theory of inference:

bayes-updating-theory-3

From this equation, we see how information updates our belief probabilities. Bayesian updating describes this transition from prior to posterior, P(H) → P(H|E).

As evidence accumulates, one’s “belief distributions” tend to become sharply peaked. Here, we see degree of belief in a hockey goalie’s skill, as we observe him play. (Image credit Greater Than Plus Minus):

bayesian_updating

What does it mean for a distribution to be uncertain? We would like to say that our certainty grows as the distribution sharpens. Unfortunately, probability theory provides no language to quantify this intuition.

This is where information theory comes to the rescue. In 1948 Claude Shannon discovered a unique, unambiguous way to measure probabilistic uncertainty. 

What is this function? And how did he discover it? Let’s find out.  

Desiderata For An Uncertainty Measure

We desire some quantity H(p) which measures the uncertainty of a distribution.  

To derive H, we must specify its desiderata, or what we want it to do. This task may feel daunting. But in fact, very simple conditions already determine H to within a constant factor. 

We require H to meet the following conditions:

  1. Continuous. H(p) is a continuous function.
  2. Monotonic. H(p) for an equiprobable distribution (that is, A(n) = H(1/n, 1/n, 1/n)) is a monotonic increasing function of n.
  3. Compositionally Invariant. If we reorganize X by bundling individual outcomes into single variables (b: X → W), H is unchanged, H(X) = H(W).

Let’s explore compositional invariance in more detail.

Deriving H

Let us consider some variable X that can assume discrete values (x_1, ..., x_n). Our partial understanding of the processes which determine X are the probabilities (p_1, ..., p_n). We would like to find some H(p_1, ..., p_n), which measures the uncertainty of this distribution.

Suppose X has three possible outcomes. We can derive W by combining events x2 and x3. 

entropy-uncertainty-composition-variables

The uncertainty of X must be invariant to such bundling. So we have that:

entropy-uncertainty-composition-example-v1

The right tree has two distributions p(W) and p(X|W). The uncertainty of two distributions is the sum of each individual uncertainty. Thus we add H(⅔, ⅓). But this distribution is reached only ½ of the time, so we multiply by 0.5.

How does composition affect equiprobable distributions A(n)? Consider a new X with 12 possible outcomes, each equally likely to occur. The uncertainty H(X) = A(12), by definition. Suppose we choose to bundle these branches by (3,5,4). Then we have:

entropy-uncertainty-composition-example-v2

But suppose we choose a different bundling function (4,4,4). This simplifies things:

entropy-uncertainty-composition-example-v3-3

For what function of A does A(mn) = A(m) + A(n) hold? There is only one solution, as shown in Shannon’s paper:

A(X) = - Klog(X)

K varies with logarithmic base (bits, trits, nats, etc). With this solution we can derive a general formula for entropy H.

Recall,

X = (x_1, ..., x_n), P(X) = (p_1, ..., p_n)

A(X) = K \log(X) ← Found by uniform bundling (eg., 4,4,4)

A(\sum{n}) = H(X) + \sum\limits_{i} \left( \frac{b_i}{\sum{n}} \right) A(b_i) ← Found by arbitrary bundling (eg., 3,5,4)

Hence,

Klog(\sum{n_i}) = H(X) + K \sum{p_i \log(n_i)}

K \left[ \sum{p_i \log(\sum{n_i})} - \sum{p_i \log(n_i)} \right]

H = -K \sum{p_i \log\left(\frac{n}{\sum{n_i}} \right)}

We have arrived at our definition of uncertainty, the entropy H(X):

H(X) = -K \sum{p_i \log(p_i)}

To illustrate, consider a coin with bias p.  Our uncertainty is maximized for a fair coin, p = 0.5, and smallest at p = 0.0 (certain tails) or 1.0 (certain heads).

entropy-uncertainty-example-graph-of-h-1

Entropy vs Information

What is the relationship between uncertainty and information? To answer this, we must first understand information.

Consider the number of possible sentences in a book. Is this information? Two books contain exponentially more possible sentences than one book.

When we speak of information, we desire it to scale linearly with its length. Two books should contain approximately twice as much information.

If we take the logarithm of the possible messages W, we can preserve this intuition:

I(X) = K \log(W) = K \sum{P(X)}

Recall that,

H(X) = -K \sum{P_i(X) \log P_i(X)}

From here, we can show that entropy is expected information:

H(X) = \sum{P_i(X) \log P_i(X)}

H = E\langle I \rangle

What does this discovery mean, though?

Imagine a device that produces 3 symbols, A, B, or C. As we wait for the next symbol, we are uncertain which symbol comes next. Once a symbol appears our uncertainty decreases, because we have received more information. Information is a decrease in entropy.

If A, B, and C occur at the same frequency, we should not be surprised to see any one letter. But if P(A) approaches 0, then we will be very surprised to see it appear, and the formula says I(X) approaches ∞. For the receiver of a message, information represents surprisal.

On this interpretation, the above formula becomes clear. Uncertainty is anticipated surprise. If our knowledge is incomplete, we expect surprise. But confident knowledge is “surprised by surprise”. 

Conclusions

The great contribution of information theory lies in a measure for probabilistic uncertainty.

We desire this measure to be continuous, monotonic, and compositionally invariant. There is only one such function, the entropy H:

H(X) = -K \sum{p_i \log(p_i)}

This explains why a broad distribution is more uncertain than one that is narrow.

Henceforth, we will view the words “entropy” and “uncertainty” as synonymous.

Related Works

  • Shannon (1948). A Mathematical Theory of Communication
  • Jaynes (1957). Information Theory and Statistical Mechanics
  • Schneider (1995). Information theory primer

An Introduction To Energy

kevinbinz 3 Comments

Part Of: Demystifying Physics sequence
Content Summary: 700 words, 7min reading time.

Energy As Universal Currency

Why does burning gasoline allow a car to move? Chemical reactions and kinetic propulsion seem quite distinct.

How does a magnet pull a nail from the ground? What relation exists between magnetism and gravitational pull?

What must occur for a nuclear reactor to illuminate a light bulb? What connection is there between nuclear physics and light waves?

Energy is the hypothesis of a hidden commonality among the above phenomena. There are many forms of energy: kinetic, electric, chemical, gravitational, magnetic, radiant. But these forms are expressions of a single underlying phenomena.

A single object may possess many different energy forms simultaneously:

A block of wood thrown into the air will possess kinetic energy because of its motion, gravitational potential energy because of its height above the ground, chemical energy in the wood (which can be burned), heat energy depending on its temperature, and nuclear energy in its atoms (this form is not readily available from our block of wood, but the other forms may be).

Non-physicists worry that physics involves memorizing a giant catalogue of phenomena, each discovered by some guy who got an equation named after him. Energy is the reason why physics is not “stamp collecting”. It allows us to seamlessly switch between different phenomena.

Change As Energy Transformation

The only thing that is constant is change.
        -Heraclitus

Certain Greek philosophers were obsessed with change. Physics gives us a language that formalizes these intuitions. Consider the following.

  • Energy is the capacity to do work; that is, initiate processes.
  • Processes (i.e., work) involve continuous and controlled actions, or changes.

A confusing diversity of phenomena can produce force (the ability to accelerate things), but they all share the same blood. Change is energy transformation.

We can play “where does the energy come from” game on literally any event in the physical universe:

energy-processes-as-energy-transmutation-1

A Worked Example

Let’s get concrete, and go through a simple illustration of work as energy transformation. 

Our example involves a ball sliding down an incline.

energy-incline-motion-example-problem-3

To get our bearings, let’s calculate the acceleration experienced by the ball

energy-incline-motion-example-acceleration-3

To demonstrate conservation of energy, we first need to solve for the ball’s final velocity (v) at the bottom of the ramp. Recall the lesson of kinematic calculus, that displacement, velocity, and acceleration are intimately related:

x(t) = \int v(t) = \int \int a(t)

a(t) = v'(t) = x''(t)

We can use these formulae to calculate final velocity (for a tutorial see here).

energy-incline-example-kinematic-solution-6

So the ball’s final velocity will be 6.26 meters per second \sqrt{4g} m/s). However, recall the classical definitions of kinetic and potential (gravitational) energy, which are KE = \frac{1}{2}mv^2 and PE = mgh.

If conservation of energy is true, then we should expect the following to hold:

(KE + PE)_{final} - (KE + PE)_{initial} = 0

Is this in fact the case? Yes!

m[(0 + 2g) - (\frac{ \sqrt{(4g)^2} }{2})] + 0 = m[2g - 2g] = 0

Total energy of the ball stays the same across these two points. Conservation of energy can also be demonstrated at any other time in the ball’s journey. In fact, we can show that potential energy is smoothly converted to kinetic energy (image credit Physics Classroom).

conservation_energy

Why is the ball transforming its energy KE \rightarrow PE? Because it is experiencing a force.

Cosmological Interpretation

Just as space and time are expressions of a single spacetime fabric, Einstein also demonstrated mass-energy equivalence. Mass is simply a condensed form of energy, capable of being released in e.g., nuclear explosions. Do not confuse mass and matter. Mass and energy are (interchangeable) properties of matter.

So there are two components of reality: energymass and spacetime. Spacetime bends for energymass. Energy is conserved, but has many faces. The laws of physics (quantum field theory and general relativity) describe the interactions between energymass and spacetime. And since we know that energy is conserved, all there is today was all there was at the beginning of time.

If the amount of energy contained in our universe doesn’t change, what is this quantity? How much energy is there? One strong candidate theory is zero. The flat universe hypothesis rests on the realization that gravitational energy is negative, and claims that it counterbalances all other mediums.

energy-flat-universe-hypothesis

Next time, we will explore the distinction between usable vs inaccessible energy. Until then.