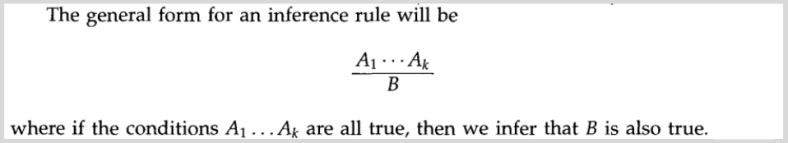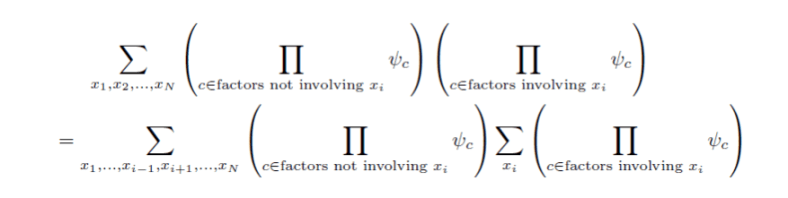Author kevinbinz

Goodman: Semiring Parsing

kevinbinz Leave a comment

Part Of: [Advanced Inference In Graphical Models] sequence

Table Of Contents

  • Introduction
  • Article Metadata
  • Item-Based Description
  • Candidate Semirings
  • Mechanizing Algorithm Construction
  • Algorithm-Metaring Diplomacy
  • Conclusion

Introduction

There are 1,024 logical permutations of rings/fields. Why is so much of the algorithmic research on them focused on one particular class of algebraic structure: the semiring? Why not the ring, or the pseudoring?

One answer can be made by appealing to historical accident. Semiring-based algorithm generation methods were championed most prominently by the Natural Language Processing (NLP) community, because the Chomsky–Schützenberger theorem unearthed deep connections between context-free grammars and certain noncommutative semiring algebras.

This post is a summary of John Goodman’s article, Semiring Parsing, which applies group theoretic techniques to already-known algorithms used by NLP researchers.

Article Metadata

  • Article: Semiring Parsing
  • Author: John Goodman
  • Published: 1999
  • Citations: 126 (note: as of 11/2014)
  • Link: Here (note: not a permalink)

Item-Based Description

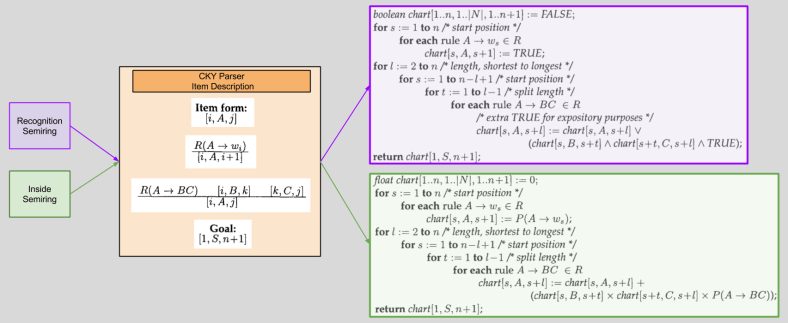
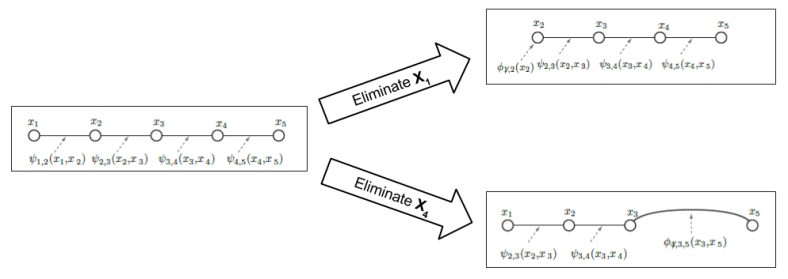
One major innovation in Goodman’s paper is item based descriptions. The syntax is straightforward:

Goodman- Item Syntax

This kind of notation simplifies the specification of parsers. More generally, as we will see, it will also free us from the traditional procedural-based approach to constructing algorithms in this domain.

Semiring Types

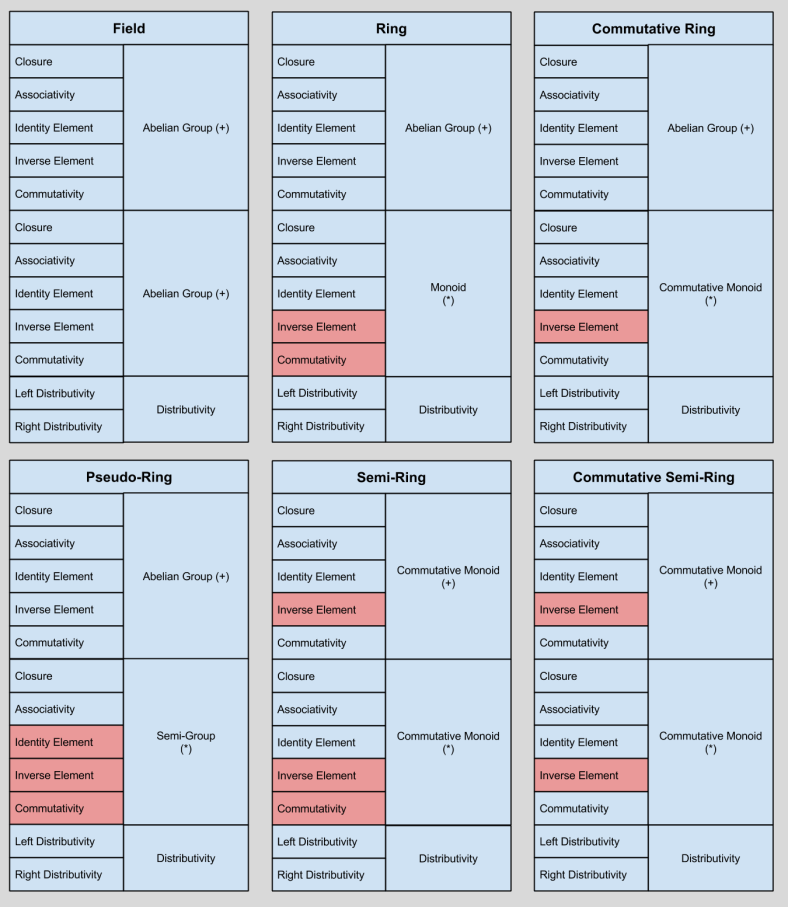
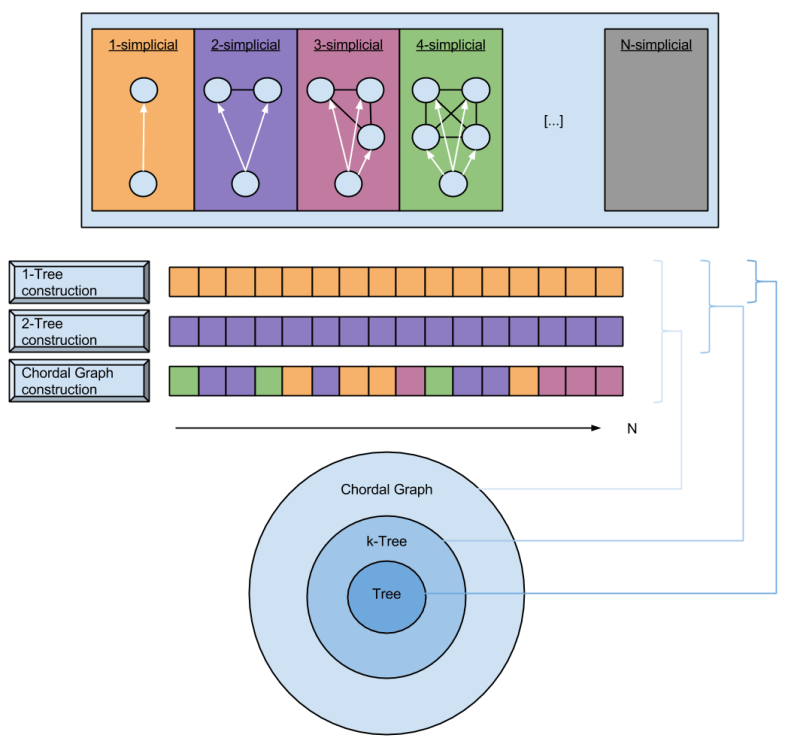
Let me call any type of permutation within a group-like structure a metagroup, and let me call any type of permutation within a ring-/field- like structure a metaring.

Another bit of background: do you remember the space of metarings? Here’s a diagram to refresh your memory:

Group Theory- Trimming Fields

Ring-like algebraic structures only have five differentiating factors: the input set over which they operator, the aggregation operator, the combination operator, and their two identity elements.

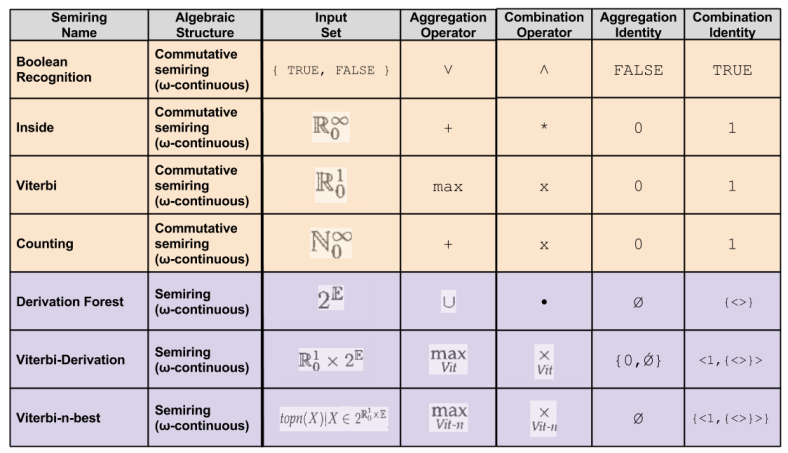
We can imagine a multitude of different permutations of these five variables. In the NLP community, seven permutations stand out as particularly valuable. They are:

Goodman- Semiring Types (3)

Mechanizing Algorithm Construction

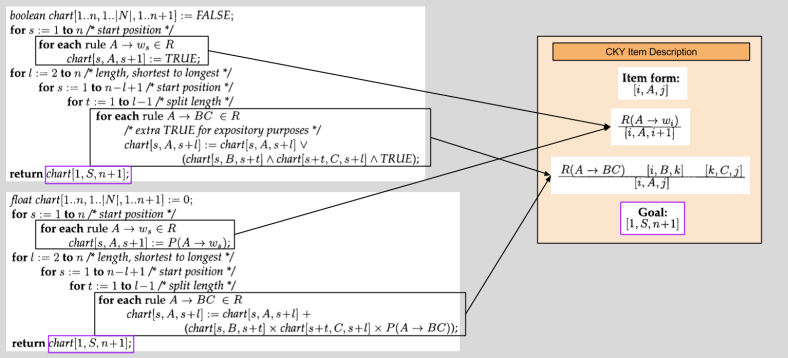
Consider the following algorithms:

Goodman- CKY recognition versus inside algorithm

Notice any similarities?

You should! The only differences between the two algorithms are substitutions between:

  • ˄ <–> *
  • ˅ <–> +
  • P(*) <–> TRUE

Let’s leverage item descriptions to generalize these two algorithms:

Goodman- Generalizing To Item-Based Description

With our new Item Description, algorithm generation becomes mechanized:

Goodman- Item-Based Description + Algebraic Structure = Algorithm

What makes this plug-and-play system more compelling than merely an ad-hoc explanation of algorithms whose existence we have already described?

Well, the Item Description doesn’t just accept these two semirings! Plug more in, and see what you get. 🙂 As Goodman puts it:

It [now becomes] easier to generalize parsers across tasks: a single item-based description can be used to compute values for a variety of applications, simply by changing semirings.

Algorithm – Metaring Diplomacy

Algorithms are often designed so that they can accept particular algebraic structures.

In typical practical Viterbi parsers, when two derivations have the same value, one of the derivations is arbitrarily chosen. In practice, this is usually a fine solution… but from a theoretical viewpoint, the arbitrary choice destroys the associative property of the additive operator, max. To preserve associativity, we keep derivation forests of all elements that tie for best.

Computing over infinite sets is one powerful reason why commutivity is a desideratum for these metarings:

For parsers with loops, i.e., those in which an item can be used to derive itself, we will also require that sums of an infinite number of elements be well defined. In particular, we will require that the semirings be complete. This means that sums of an infinite number of elements should be associative and commutative, just like finite sums, and that multiplication should distribute over infinite sums, just as it does over finite ones.

Commutativity is shed in the three derivation-based semirings, for the simple reason that its multiplicative operator is designed to be order-preserving:

These semirings, unlike the other semirings described in Figure 5, are not commutative under their multiplicative operator, concatenation.

Swapping out semirings is not the only strategy to exploring parser diversity. One can also swap out the sets within the Item Descriptions.

Notice that each of the derivation semirings can also be used to create transducers. That is, we simply associate strings rather than grammar rules with each rule value. Instead of grammar rule concatenation, we perform string concatenation. The derivation semiring then corresponds to nondeterministic tranductions; the Viterbi semiring corresponds to a probabilistic transducer; and the Viterbi-n-best semiring could be used to get n-best lists from probabilistic transducers.

Think only two operators are allowed in a metaring? Think again!

Notice that [in the above example] we have multiplied an element of the semiring, V(D), by an integer, C(D, x). This multiplication is meantto indicate repeated addition, using the additive operator of the semiring. Thus, for instance, in the Viterbi semiring (max-product), “multiplying” (repeat-“addition”) by a count other than 0 has no effect, since x “+” x = max(x, x) = x. Whereas in the inside semiring (sum-product), repeat-“addition” corresponds to actual multiplication.

An interesting connection between finite-state automata and HMMs:

Nondeterministic finite-state automata (NFAs) and HMMs turn out to be examples of the same underlying formalism, whose values are simply computed in different semirings. Other semirings lead to other interesting values… For NFAs, we can use the boolean semiring to determine whether a string is in the language of an NFA; we can use the counting semiring to determine how many state sequences there are in the NFA for a given string; and we can use the derivation forest semiring to get a compact representation of all state sequences in an NFA for an input string. A single item-based description can be used to find all of these values.

Goodman in his paper calls for an extension of item-based descriptions:

It would be interesting to try to extend item-based descriptions to capture some of the formalisms ocvered by Koller, McAllester, and Pfeffer, including Bayes’ nets.

Conclusion

My Open Questions:

  • Have item-based descriptions since been extended? Is there active research on this front?

Concluding Quote:

In summary, the techniques of this paper will make it

  1. easier to compute outside values,
  2. easier to construct parsers that work for any ω-continuous semiring, and
  3. easier to compute infinite sums in those semirings.

In 1973, Teitelbaum wrote:

“We have pointed out the relevance of the theory of algebraic power series in noncommuting variables in order to minimize further piecemeal rediscovery”

We hope that this paper will bring about Teitelbaum’s wish.

An Introduction To Newcomb’s Paradox

kevinbinz Leave a comment

Part Of: Algorithmic Game Theory sequence
Related To: An Introduction To Prisoner’s Dilemma
Content Summary: 1000 words, 10 min read

The Paradox

Newcomb’s Paradox is a thought experiment popularized by philosophy superstar Robert Nozick in 1969, with important implications for decision theory:

A superintelligence from another galaxy, whom we shall call Omega, comes to Earth and sets about playing a strange little game. In this game, Omega selects a human being, sets down two boxes in front of them, and flies away.

Box A is transparent and contains a thousand dollars.

Box B is opaque, and contains either a million dollars, or nothing.

You can take both boxes, or take only box B.

And the twist is that Omega has put a million dollars in box B iff Omega has predicted that you will take only box B.

Omega has been correct on each of 100 observed occasions so far – everyone who took both boxes has found box B empty and received only a thousand dollars; everyone who took only box B has found B containing a million dollars. (We assume that box A vanishes in a puff of smoke if you take only box B; no one else can take box A afterward.)

Before you make your choice, Omega has flown off and moved on to its next game. Box B is already empty or already full.

Omega drops two boxes on the ground in front of you and flies off.

Do you take both boxes, or only box B?

Well, what’s your answer? 🙂 Seriously, make up your mind before proceeding. Do you take one box, or two?

Robert Nozick once remarked that:

To almost everyone it is perfectly clear and obvious what should be done. The difficulty is that people seem to divide almost evenly on the problem, with large numbers thinking that the opposing half is just being silly.

The disagreement seems to stem from the contradiction of two strong intuitions: one “altruistic” intuition in favor of 1-box, the other 2-box intuition is more “selfish”. They are, respectively:

  1. Expectation Intuition: Take the action with the greater expected outcome.
  2. Maximization Intuition: Take the action which, given the current state of the world, guarantees you a better outcome than any other action.

Allow me to visualize the mechanics of this thought experiment now (note that the Predictor is a not-necessarily-omniscient version of Omega):

Newcomb's Paradox- Setup

Still with me? 🙂 Good. Let’s see if we can use game theory to mature our view of this paradox.

Game-Theoretic Lenses

Do you remember Introduction To Prisoner’s Dilemma? At one point in that article, we decomposed the problem into a decision matrix. We can do the same thing for this paradox, too:

Newcomb's Paradox- Decision Matrix

From the perspective of the Decider, strategic dominance here cash out our Intuition #1: the bottom row always outperforms the top row.

However, the point of making the Predictor knowledgeable is that landing in the gray cells (top-right, bottom-left) become unlikely. Let us make the size of our boxes represent the chance that they will occur.

Newcomb's Paradox- Predictive Accuracy Weighting

With a Predictor of infinite accuracy,  the size of the gray cells becomes zero, and now 1-Boxing suddenly dominates 2-Boxing.

With a Predictor with bounded intelligence, what follows? Might some logic be constructed to describe optimal choices in such a scenario?

A Philosophical Aside

Taken from this excellent article:

The standard philosophical conversation runs thusly:

  • One-boxer: “I take only box B, of course. I’d rather have a million than a thousand.”
  • Two-boxer: “Omega has already left. Either box B is already full or already empty. If box B is already empty, then taking both boxes nets me $1000, taking only box B nets me $0. If box B is already full, then taking both boxes nets $1,001,000, taking only box B nets $1,000,000. In either case I do better by taking both boxes, and worse by leaving a thousand dollars on the table – so I will be rational, and take both boxes.”
  • One-boxer: “If you’re so rational, why ain’cha rich?”
  • Two-boxer: “It’s not my fault Omega chooses to reward only people with irrational dispositions, but it’s already too late for me to do anything about that.”
  • One-boxer: “What if the reward within box B are something you could not leave behind? Would you still fall on your sword?”

Who wins, according to the experts? No consensus exists. Some relevant results, taken from a survey of professional philosophers:

Newcomb’s problem: one box or two boxes?

Accept or lean toward: two boxes 292 / 931 (31.4%)
Accept or lean toward: one box 198 / 931 (21.3%)
Don’t know 441 / 931 (47.4%)

Prediction Is Time Travel

There is a wonderfully recursive nature to Newcomb’s problem: the accuracy of the predictor stems from it modelling your decision machinery.

Newcomb's Paradox- Decision Process Leakage

In this (more complete) diagram, we have the Predictor building a model of your cognitive faculties via the proxy of behavior.

As the fidelity of its model (gray image in the Predictor) improves as more information is pulled from the Decider (red arrow) the more perfect its predictive accuracy, (reduced size of the gray outcome-rectangles).

The Decider may say to herself:

Oh, if only my mind were such that the “altruistic” Expectation Intuition could win at prediction-time, but the “selfish” Maximization Intuition could win at choice-time.

Then, I would deceive the Predictor. Then, I would win $1,001,000.

But even if she possesses the ability to control her mind in this way, a perfect Predictor will learn of it. Thus, the Decider may reason:

If my changing my mind is so predictable, perhaps I might find some vehicle to change my mind based on the results of coin-flip…

What the Decider is trying to do, here, is a mechanism to corrupt the Predictor’s knowledge. How might a Predictor respond to such attacks of deterministic prediction?

Open Questions

This article represents more of an exploration, than a tour of hardened results.

Maybe I’ll produce revision #2 at some point… anyways, to my present self, the following are open questions:

  • How can we get clear on the relations between Newcomb’s Paradox and game theory more generally?
  • How might the “probability mass” lens be used to generalize this paradox to non-perfect Predictors
  • How might the metaphysics of retroactive causality, or at least the intuitions behind such constructs, play into the decision?
  • How much explanatory power does the anti-maximization principle behind 1-boxing (and the ability to precommit to such “altruistic irrationality”) say about human feelings of guilt or gratitude?
  • How might this subject be enriched by complexity theory, and metamathetics?
  • How might this subject enrich discussions of reciprical altruism and hyperbolic discounting?

Until next time.

Tree, Generalized

kevinbinz Leave a comment

Part Of: [Advanced Inference In Graphical Models] sequence
Followup To: [An Inference Trail To Chordal Graphs]

Table Of Contents

  • Context
  • Parallels Between Trees and Chordal Graphs
  • Parameterizing Simpliciality
  • Definition By Construction
  • K-trees
  • Takeaways

Parallels Between Trees And Chordal Graphs

In Murderous Messages, we defined perfect elimination orderings as follows:

Let perfect elimination ordering (PEO) refer to exact inference algorithms that do not at any step introduce fill-in edges; F = {}. In order to accomplish such an ordering, we should eliminate nodes that match either one of two elimination principles:

  • have only zero or one neighbor (leaf nodes)
  • have neighbors that are already fully connected. (simplicial nodes)

In our inference trails towards both trees and chordal graphs, we came upon the following similar-looking properties:

  • Every tree with size > 1 has two leaf nodes (nodes in a tree with only one neighbor).
  • A chordal graph is either a clique, or at least two non-adjacent nodes are simplicial. [Lemma 30]

Note the implication that you’ll never run out of leaf/simplicial nodes to eliminate: every time you remove a leaf/simplicial node, the resultant tree/graph still retains this two-target characteristic. Since you are assured leaves/simplicials “all the way down”, this guarantees that both trees and chordal graphs may sustain perfect elimination orders. And that is nice.

We proceeded to author construction-based definitions of these data structures. Note again how frustratingly similar they are, despite their independent derivations!

  • T is a tree if it is generated via the following process: Start with a node v. Repeatedly choose a next vertex, and connect it with an edge to exactly one previously chosen vertex.
  • G is a chordal graph if generated via the following process: Start with a clique. All chordal graphs can be generated by connecting the next node to some set of previously-chosen nodes that are a clique. [Corollary 36]

Parameterizing Simpliciality

Let’s transcend an appeal to coincidence: why have two things when we can have one? 😛

Time to consolidate. Recall our definition of simplicial node?

Simplicial node: a node whose neighbors form a clique.

Let’s make this definition more granular, and define a concept that hinges on the size of this neighbor-clique.

k-simplicial node: a node whose neighbors form a clique of size k.

Here’s how this looks “in action”:

EE512 Generalizing Trees- N-simplicials

A few notes about the boundaries of this distribution:

  • What is the maximum size of an k-simplicial node? When the entire graph is a clique, when k = N (the number of all nodes). k spans [1..N].
  • Does a 1-simplicial node remind you of anything? It should. Creating a 1-simplicial node is equivalent to appending a leaf node.

Definition By Construction

With this definition of k-simplicials in hand, let’s return to our twin construction properties mentioned above.

  • T is a tree if generated via the following process: Start with a node v. Repeatedly choose a next vertex, and connect it with an edge to exactly one previously chosen vertex.
  • G is a chordal graph if generated via the following process: Start with a clique. All chordal graphs can be generated by connecting the next node to some set of previously-chosen nodes that are a clique. [Corollary 36]

Now, we can represent this graphically by realizing that the former process is about consistently appending 1-simplicials, and the latter process fueled by k-simplicials. The distinction, then, looks like this:

 

EE512 Generalizing Trees- Tree Construction Basics (1)

k-Trees

In our visualization of tree construction, did you notice how the color of tree construction doesn’t change? Let’s generalize this property beyond orange (1-simplicials).

Let k-tree represent a tree whose construction process is fueled by k-simplicials. I illustrate four of these tree abstractions here:

EE512 Generalizing Trees- k-Trees

Are there k-trees that are not chordal graphs? How do k-trees generally relate to our previous concepts of trees and chordal graphs? Another illustration should clarify these inter-relationships:

EE512 Generalizing Trees- Tree Hierarchy

A tree is a subset of a k-tree which is a subset of chordal graphs. We know this because:

  • A chordal graph is constructed by (any chain of) simplicials
  • A k-tree is constructed by (one consistent chain of) simplicials.
  • A tree is constructed by (one particular consistent chain of) simplicials.

Takeaways

  • A leaf node is synonymous with a simplicial node of size 1.
  • A k-tree is a tree constructed with simplicial nodes of size k (a 1-tree is synonymous with a tree, per the above identity).
  • A tree is a kind of k-tree which is a kind of chordal graph: these three data structures are strict subsets of one another.

Here’s a consolidation of the above images, for convenience:

EE512 Generalized Trees- Summary Infographic (1)

Designer Families

kevinbinz Leave a comment

Part Of: [Advanced Inference In Graphical Models] sequence
Followup To: [Family vs. Universe]

Table Of Contents

  • Motivations
  • Graph Type: Factor Graphs
  • Graph Type: Markov Random Fields
  • A Tale Of Three Families
  • On Specificity
  • Takeaways

Motivations

Today, we’re going to talk through the construction of a family, and how such a construction might succeed or fail.

Across machine learning, there exist dozens of different graph types; of these, three are the most popular:

  1. Markov Random Fields
  2. Factor Graphs
  3. Bayesian Networks

Our example today will span the first two of these graphs.

Graph Type: Markov Random Field

Markov Random Fields (MRFs) have very simple semantics; they are basically undirected graphs:

EE512 Designer Families- MRF Example

 

In the above MRF, we have a graph with five vertices and six edges. It’s probability distribution is comprised of three factors, one per maximal clique (the first term corresponds to top-left triangle, etc).

The graphical model of MRFs can be formalized by defining its graph and rule structure. Let us define the following terms:

  • Let V represent the set of all vertices in the graph
  • Let E represent the set of all edges in the graph

We now define the Markov Random Field:

EE512 Designer Families- MRF Theory

Here’s how I “translate” all the math on the right:

  • “For each cliques in the set of all maximal cliques, there exists a function phi over some collection of variables within the clique.”
  • “The joint probability, then, over all variables is the product of all  phi functions in the graph.”

It turns out that there are several other rules which describe an MRF equally well, but maximal-clique factorization rule serves our purposes here well enough.

Introducing Factor Graphs

Factor graphs (FGs) also have undirected edges, but they honor other constraints, as well:

EE512 Designer Families- Factor Graphs Example

Notice anything interesting about this graph’s edges? […] Did you notice how no v-nodes or f-nodes are never connected one another? In other words, if we group all edges Graphs with this property, that all edges span across two distinct nodesets, are called bipartite graphs.

How is the probability distribution formula constructed? […] On inspection, it becomes clear that each of the four terms on the right-hand side correspond to factor-nodes.

A rigorous definition of factor graphs simply require us to generalize these two observations. First, some vocabulary is in order.

  • Let V represents the set of vertex-nodes on the graph (e.g., v1 through v3)
  • Let F represent the set of factor-nodes on the graph (e.g., f1 through f4)
  • Let E represent the set of all edges in the graph.

We are now in a position to completely specify the Factor Graph:

EE512 Designer Families- Factor Graphs Theory

Here’s how I would translate this family definition:

  • “Let neighbor function RHO be defined as a function that searches through each factor and returns each neighbor.”
  • “For every factor f, there exists a function PSI, which takes as its input all neighbors of f (those neighbors discovered by RHO).”
  • “The joint probability is then the product of all such functions PSI.”

 A Tale Of Three Families

Ready to get your hands dirty?! Good! Let’s consider three specific graphs: two factor graphs, and one Markov Random Field:

EE512 Designer Families- Three Families

Does this diagram make sense? If not, let me explain each family-distribution pairing in turn.

  • The leftmost family represents the semantics of factor-graphs R(fg), along with a set of factor-nodes, vertex-nodes, and edges G1. Just as in the factor-graph example above, its corresponding probability distribution is derived from these two elements: each term corresponding to one factor-node and its neighbors.
  • The center family is identical to the previous factor-graph, except for an additional factor-node. This additional element corresponds to an extra term in the resultant probability distribution, f4(…)
  • The rightmost family represents the semantics of MRFs (here, maxclique factorization) R(mcf), along with a set of nodes and edges G3. Its probability distribution flows from the semantics: since all three variables form a clique, the distribution is a factor across all variables.

So far, so obvious. But recall the purpose of rules: they deliver yes/no answers to any probability distribution that applies for membership. Thus, we must be willing in inquire whether p1 is a member of Family2, etc.

Here are the membership results of the six new family applications:

EE512 Designer Families- Three Families With Exclusions

 

A green edge (A, B) means that our Ath distribution is a member of our Bth family. In contrast, a red edge denotes non-membership. Let me explain the results of each new edge in turn:

  1. (1,2) is green because f(a, b) -> g(x, y, z) transforms are possible.
  2. (1,3) is green because f(a, b) -> g(x, y, z) transforms are possible.
  3. (2,1) is red because f(a, b, c) -> g(x, y) transforms are impossible (if they were, they would be expressed as two-term factors originally).
  4. (2,3) is green because f(a, b, c) -> g(x, y, z) transforms are possible.
  5. (3,1) is red because f(a, b, c) -> g(x, y) transforms are impossible (similar reasoning to (2,1)).
  6. (3,2) is green because f(a, b, c) -> g(x, y, z) transforms are possible.

On Specificity & Generality

Consider you find yourself asked to design an graphical model that includes p1 within its family. As you can see, any of the above graphs satisfy this requirement. But that does not make them equal.

When designing families, we ought to be as narrow as possible. Suppose we don’t particularly care to compute over p2 or p3. Then, we have reason to prefer Family1 asdf – it has the power to say No to these irrelevant distributions, and thereby save computational resources.

Here’s how my professor summarizes & illustrates this principle:

This suggests that there are two aspects of a type of graphical model that indicate its power, and that is: generality, can a graph be found such that its family includes a given distribution; and specificity, how discriminative is a given graph that represents a given distribution.

For example, a collection of all i.i.d. random variables would trivially be a member of all of the aforementioned families, but such a distribution would violate many of the properties that are left unspecied. We might be interested in another graphical model semantics that specifically precludes those cases.

These two notions help us get clear on the kinds of questions to ask when designing a graphical model from scratch.

Takeaways

  • When designing a family, one must optimize not just for generality (admitting viable distributions). Specificity (the rejection of irrelevant distributions) matters just as much.

Murderous Messages

kevinbinz Leave a comment

Part Of: [Advanced Inference In Graphical Models] sequence
Followup To: [Murderous Cliques]

Table Of Contents

  • Context
  • Forests & Trees
  • Perfect Elimination
  • Murderous Messages
  • Takeaways

Context

Our takeaways from last time:

  • Cliques are graph subsets that are fully connected.
  • Variable elimination is a computational process that first bundles like factors together, and then eliminates a variable via “summing it out”.
  • The order in which one eliminates irrelevant variables is computationally significant.
  • Sometimes, variable elimination creates undesirable fill-in edges – edges that breach the family contract & expands the boundaries of the graphical model.
  • Fill-in edges happen because the former neighbors of a fill-in edge must form a clique.
  • In conclusion, when selecting the order in which to eliminate variables, if possible, choose the variable whose neighbors already form a clique.

We can make our conclusion more specific.

Let perfect elimination ordering refer to exact inference algorithms that do not at any step introduce fill-in edges; F = {}.

In order to accomplish such an ordering, we should eliminate nodes that match either one of two elimination principles:

  1. have only zero or one neighbor
  2. have neighbors that are already fully connected.

In either case, fill-in edges will not be added because the clique requirement is already satisfied.

Forests & Trees

So far in this sequence, we have considered a wide variety of different graph types. Today, let us consider a special type of graph: the forest, and the tree.

Informally, a forest is a graph that has no cycles. A tree is a connected forest, a forest in which two nodes are connected by precisely one path.

Below is one forest comprising four trees:

EE512 Messages- Tree Illustration

 

Theorem 2 (Trees, Berge). Let T = (V, E) be an undirected graph with |V| = n > 2. Then each of the following properties are equivalent and each can be used to define a tree.

  1. G is connected, and has no cycles.
  2. G has n – 1 edges and has no cycles.
  3. G is connected and contains exactly n-1 edges.
  4. G has no cycles, and if an edge is added to G, exactly one cycle is created.
  5. G is connected, and if any edge is removed, the remaining graph is not connected.
  6. Every pair of vertices of G is connected by one unique path.
  7. G can be generated via the following process: Start with a node v. Repeatedly choose a next vertex, and connect it with an edge to exactly one previously chosen vertex.

Perfect Elimination

Do all graphs support a perfect elimination ordering (PEO)? Consider the following:

EE512 Messages- PEO Examples

In the left image, a PEO does not exist: it doesn’t matter which node you chose, its two neighbors are not already-connected. The right image, in contrast, does contain a PEO (as was shown last time).

Notice how the left 4-cycle is not a tree, whereas the right chain is. Might other types of trees (besides chains) also support perfect elimination orderings? The answer turns out to be yes:

  • The maximum clique size of a tree is 2 (cliques of size three would form a cycle, and trees do not contain cycles).
  • Every tree with size > 1 has 2 leaf nodes (nodes in a tree with only one neighbor).
  • Variable elimination on trees do not destroy their tree-like nature.
  • If you always choose to eliminate an edge node first, the neighboring clique is of size 1, which guarantees F = {}. Let us call this procedure leaf-first ordering.
  • Locating leaf nodes on a tree is computationally straightforward.

Therefore, any leaf-first ordering on a tree will yield a perfect elimination order, and operate in O(N*r^2) time.

Two important facts to remember:

  1. The leaf-first ordering procedure does not specify one particular ordering as correct. Rather, it denotes a group of orderings as equivalent and correct.
  2. As a data structure, trees were chosen because they guarantee elimination principle #1.

Murderous Messages

Time to view leaf-first ordering in action. Consider a tree T with |V| = 15. Suppose that, after building this tree with statistical data, a scientist submits a query as to the relationship between two variables.

We know how to perform this inference: eliminate all variables not involved in the query itself. To perform such elimination perfectly, we perform leaf-first ordering:

EE512 Messages- Murderous Messages

In the right image, we “rooted” T on the query variables, and eliminated the irrelevant nodes starting from the “lowest” ones.

Pay attention to the way information flows with the above ordering. It is as if the query variables act as a collecting magnet, sucking information from the rest of the graph towards its nodes. On a Bayesian interpretation of this algorithm, we can meaningfully state that this leaf-first ordering is a collection of evidence. Let us call such transmission of evidence message passing.

We can then re-interpret leaf-first ordering in the following protocol:

Message Passing Protocol (MPP): A message may be sent from node i to a neighbor node j only after node i has received a message from all of its other neighbors.

We motivated the MPP based on trees, and elimination principle #1. But we will later MPP in the context of chordal graphs, which guarantee principle #2.

Two things to bear in mind as we close:

  • The phrase murderous messages is simply a playful concatenation of the more cantankerous “variable elimination message passing”.
  • Notice how the requirement for maximal efficiency (in the form of perfect elimination ordering) is what motivated us to connect an inference algorithm with notions of epistemic fidelity.

Takeaways

  • A forest is a graph that has no cycles. A tree is a connected forest.
  • In trees, perfect elimination ordering is accomplished by leaf-first ordering.
  • Leaf-first ordering can be reasonably interpreted as the collection of evidence (a.k.a message passing, or belief propagation).

Murderous Cliques

kevinbinz Leave a comment

Part Of: [Advanced Inference In Graphical Models] sequence

Table Of Contents

  • Cliquish Nodes
  • The Mechanics Of Variable Elimination
  • A Question Of Order
  • Enter Graphical Models
  • Murderous Cliques
  • Takeaways

Cliquish Nodes

Fully-connected networks have some interesting properties. Let’s create a vocabulary to reason about them in more nuanced graphs.

  • Let clique be a subset of nodes in a graph that are fully connected. Call the set of all cliques C.
  • Let maximal clique be a clique that cannot remain a clique by including any one more adjacent vertex.
  • Let maximum clique be a clique Cmm for which |Cmm| =  max(|Cx|) for each Cx in C.

An example may help, you say?!

EE512 Cliques- Clique IllustrationOur three sets in action:

  • Cliques: {{1}, {2}, {3}, {4}, {5}, {1, 2}, {2, 3}, {1, 3}, {2, 4}, {3, 4}, {2, 5}, {1, 2, 3}, { 2, 3, 4 }}
  • Maximal Cliques: {{1, 2, 3}, {2, 3, 4}, {2, 5}}
  • Maximum Cliques: {{1, 2, 3}, {2, 3, 4}}

The Mechanics Of Variable Elimination

The basic point of variable elimination is to push summation signs as far to the right as possible, to reduce computational complexity (you no longer have to ask factors not involving xi, to sum over it).

Let us call this the factor grouping step:

EE512 Cliques- Factor GroupingSee how we pulled xi summation to the right?

Once we have a single summation over only the relevant factors, we proceed. The resultant aggregation will no longer contain Xi; therefore, let us call this operation variable elimination step.

EE512 Cliques- Variable Elimination

To be clear, the above notation is a psi1, 2 – but the one is scratched out, to represent its elimination.

Putting these two steps together, we can now understand the process of eliminate a variable from our model. Consider the task of eliminating x1 from the following model:

EE512 Cliques- VarElim Example

The above image captures the process for eliminating one variable. To find p(x3, x4), we must eliminate two more. Imagine we choose X5 to eliminate next, and then X2.  The resulting equation will bear our answer, the value of p(x3, x4).

A Question Of Order

In the above example, we chose the following variable elimination ordering: (1, 5, 2). But other orderings are possible. How does (1, 5, 2) compare to (2, 1, 5) or (5, 2, 1)?

How might we rank the desirability of different variable elimination orderings? An attractive metric is computational complexity: we should choose the ordering that minimizes the amount of required CPU muscle.

Enter Graphical Models

Graphical models provides us a way to visually inspect what used to be solely manipulations of formulae. Here is the exact same computation as above, but with pictures:

EE512 Cliques- Elimination Ordering - Edge First

The key insight: the reconstituted graphical model (GM) is equivalent to the original GM.

HOWEVER! Such equivalence is not guaranteed! Consider what happens when we eliminate X4 first:

EE512 Cliques- Elimination Ordering - Non-Edge First

Notice how the reconstituted GM diverges from the original GM: a new edge has been added between x3 and x5. Let us call this a fill-in edge.

Fill-in edges are bad news. The edges of the original graph constitute its family: when you add edges, the boundaries of the family expands, which hurts inference processes. Recasting our lens to asymptotic analysis, fill-in edges represent an added computational burden – tables whose dimensionality we would rather not compute over.

Why does choosing to first eliminate X4 create a fill-in edge? To understand these, we’ll need to apply deep mathematics to analyze relationships between different families F(G, R).

Murderous Cliques

Let us use MRF-clique semantic interchangeability to look at fill-in edges with the lens of clique semantics. Consider again the fill-in edge phenomenon encountered above:

EE512 Cliques- Elimination Ordering - Fill-In Edge Consequences

In the original graph (left), the maximal cliques are {{1, 2}, {2, 3}, {3, 4}, {4, 5}}. The key insight is as follows:

  • Existence of f1(xA, xB) suggests that G[A ∪ B] should be a clique, and existence of f2(xB, xC) suggests G[B ∪ C] should be a clique.
  • After summation, existence of f(xA, xC) suggests that G[A ∪ C] should also be a clique (if it is not already).

In other words:

  • After v is eliminated, all of its former neighbors must form a clique. If they do not, undesirable fill-in edges will be added to our graph, and the family will expand.

We can explain the x4 fill-in edge because its neighbors (x3 and x5) were not already a clique.

Thus, variable elimination ordering becomes a question of analyzing the cliques of a graph. Let us call this perspective murderous cliques for short! 🙂

Takeaways

  • Cliques are graph subsets that are fully connected.
  • Variable elimination is a computational process that first bundles like factors together, and then eliminates a variable via “summing it out”.
  • The order in which one eliminates irrelevant variables is computationally significant.
  • Sometimes, variable elimination creates undesirable fill-in edges – edges that breach the family contract & expands the boundaries of the graphical model.
  • Deep parallels exist between clique semantics and traditional MRF factoralization.
  • Fill-in edges happen because the former neighbors of a fill-in edge must form a clique.
  • In conclusion, when selecting the order in which to eliminate variables, if possible, choose the variable whose neighbors already form a clique.

Family vs. Universe

kevinbinz 1 Comment

Part Of: [Advanced Inference In Graphical Models] sequence

Table Of Contents

  • Definitions Make The World Go ‘Round
  • Searching The Universe
  • The Topography Of Truth
  • Redemption Via Solution-Space Constraint

Definitions Make The World Go ‘Round

Agents within the particle soup of the universe may sample its contents.

  • Let the random variables X1, …, XN represent such samples of reality. (I discuss random variables in more depth here.)
  • Let the joint probability p(X1, …, XN) represent our belief about the whole system.
  • Let the universe U represent all possible p(X1, …, XN) distributions.

Searching The Universe

How big is U? Well, let’s imagine a simple case, where N = 3, and the domain of every random variable is {true, false}.

EE512- Joint Prob Example

Two things to notice in the above joint probability table:

  • We use the X1 to refer to the variable, and x1 to refer to its value.
  • The summation of all p(x1, x2, x3) rows equals 1.0 (translation: “there is a 100% chance that all variables will have some value”).

The Topography Of Truth

Our probability function must generate a value for every permutation of random variable values. Using the |*| notation to represent a “size/number of” operator, we find that |rows| = |domain|^|variables|. This equation explains why we have eight rows: 8 = 2^3.

But what happens when N is larger than 3? For any N, the number of rows we must use to provide p(X1, …, XN) is 2^N. But exponential growth is not computationally tractable. Intractability means that any computational system – brain or CPU – cannot hope to traverse U efficiently.

The above line of reasoning is called asymptotic analysis. But there exists another way to reason about tractability. 

Imagine there exists a distribution ptrue(x1, …, xN) that our search algorithm tries to locate within U. But ptrue(x1, …, xN) is just one distribution out of many. We can represent the situation with a solution landscape:

  • The x and y dimensions (width, breadth) encode locations of different probability distributions
  • The z dimension (height) encode some metric of distribution accuracy.

In our solution landscape, ptrue(x1, …, xN) is simply the highest peak in the landscape, and our search algorithms’ task is simply to locate it. We can call this process gradient ascent.

Tractable landscapes tend to be convex, with no local minima; therefore, gradient ascent will lead to the ptrue(x1, …, xN) peak. Intractable landscapes tend to be, well… more chaotic.

Tractability- Topography Landscapes

In such unforgiving terrain, it becomes clear why searching U, even via sophisticated approximation algorithms, tends to yield inadequate solutions.

Redemption Via Solution-Space Constraint

Let a graph comprise a set of vertices V, and a set of edges E. A graphical model, then, is the conjunction of a graph with a set of rules R.  More formally:

  • G = (E, V)
  • GM = (G, R) = ((E, V), R)

What type of rules comprise R? I discuss cognitive versions of such rules here.

R are a set of rules that map from graph G to statements about probability distributions. An individual rule r is a predicate (truth statement) that takes a graph and a probability distriution, and evaluates to either true or false.

In practice, the rules in R tend to encode conditional independence. The important point, though, is that R constrains U. The set of probability distributions that conform to the rules of some graphic model is smaller than the set of all possible distributions. Let F represent a family of distributions, a subset of all possible distributions U.

More importantly, the rules of a graphical model are carefully designed to yield a tractable family of the solution space. Thus, solution space looks like:

EE512- Family vs. Universe Sets

To paraphrase my professor:

Sometimes it’s better to find an exact solution to an approximate problem [exact inference on F] than to find an approximate solution to an exact problem [approximate inference on U].

 

[Sequence] Graphical Models

kevinbinz Leave a comment

Hi! So, I’m trying out something new. It’s no longer summer, which means I have much less time to follow my own research paths (because class). But this quarter, I want to “live blog” my insights as I go along. The class is:

Lecture Posts

Exact Inference On Approximate Problem:

  • Chordal Graphs [Graphic]. Trees aren’t the only thing supporting perfect elimination orderings (PEOs). An infographic describing the chain of mathematical proofs which ultimately establish chordal graphs as supporting PEOs via the concept of minimal separators.
  • Family vs. Universe. Graphical models conjoin graphs with a set of rules, which sample & thereby constrain the entire universe U (solution-space). The constrained solution-space is called a family F.
  • Designer Families. A concrete walkthrough of family design,  including which heuristics are important to bear in mind.
  • Murderous Cliques. How cliques give us insight into making good variable-elimination-ordering choices.
  • Murderous Messages.  Graphs with no cycles (trees) allow us to re-interpret variable elimination epistemically, as a form of message passing.
  • Tree, Generalized. Introduces k-trees, and discusses the relationship between trees, k-trees, and chordal graphs.

Approximate Inference on Exact Problems:

Final Project Posts

Iterated Schizophrenic’s Dilemma

kevinbinz Leave a comment

Part Of: Breakdown of Will sequence
Followup To: Rule Feedback Loops
Content Summary: 1300 words, 13 min read

Context

Here’s where we landed last time:

  • Preference bundling is mentally implemented via a database of personal rules (“I will do X in situations that involve Y).
  • Personal rules constitute a feedback loop, whereby rule-compliance strengthen (and rule-circumvention weakens) the circuit.

Today’s post will draw from the following:

  1. An Introduction To Hyperbolic Discounting discusses warfare between successive selves (e.g., OdysseusNOW restricts the freedoms of OdysseusFUTURE in order to survive the sirens).
  2. An Introduction To Prisoner’s Dilemma discusses how maths can be used to describe the outcome of games between competitors.

Time to connect these threads! 🙂 Let’s ground our warfare narrative in the formal systems of game theory.

Schizophrenic’s Dilemma

First, we interpret { larger-later (LL) vs. smaller-sooner (SS) } rewards in terms of { cooperation vs. defection } decisions.

Second, we name our actors:

  • P represents your present-self
  • F represents your future-self
  • FF represents your far-future-self, etc.

Does this game suffer from the same issue as classical PD? Only one way to find out!

ISD- Simple Example (1)

Here’s how I would explain what’s going on:

  • Bold arrows represent decisions, irreversible choices in the real world. Decisions lock in final scores (yellow boxes).
  • Skinny arrows represent intentions, the construction of rules for future decisions.
  • The psychological reward you get from setting intentions is just as real as that produced by decisions.
  • Reward is accretive: your brain seeks to maximize the sum total reward it receives over time.

Take some time to really ingest this diagram.

Iterated Schizophrenic’s Dilemma (ISD)

Okay, so we now understand how to model intertemporal warfare as a kind of “Schizophrenic’s Dilemma“. But we “have to live with ourselves” — the analogy ought to be extended across more than one decision. Here’s how:

ISD - From Flat Behavior To IPD

Time flows from left to right. In the first row, we see that an organism’s choices are essentially linear. For each choice, the reasoner selects either an LL (larger-longer) or an SS (smaller-sooner) reward. How can this be made into a two-dimensional game? We can achieve this graphically by “stretching each choice point up and to the left”. This move ultimately implements the following:

  • Temporal Continuity: “the future-self of one time step must be equivalent to the present-self of the next time step”.

It is by virtue of this rule that we are able to conceptualize the present-self competing against the future-self (second row). The third row simply compresses the second into one state-space.

Let us call this version of the Iterated Prisoner’s Dilemma, the Iterated Schizophrenic’s Dilemma. For the remainder of this article, I will use IPD and ISD to distinguish between the two.

The Lens Of State-Space

We have previously considered decision-space, and outcome-space. Now we shall add a third space, what I shall simply call state-space (very similar to Markov Decision Processes…)

ISD- Three IPD Spaces (1)

You’ll notice that the above state-space is a fully-connected graph: in IPD, any decision can be made at any time.

But this is not true in ISD, which must honor the rule of Temporal Continuity. For example, (C, C) -> (D, C) violates that “the future-self of one time step must be equivalent to the present-self of the next time step”.  The ISD State-Space results from trimming all transitions that violate Temporal Continuity:

ISD- ISD vs IPD state spaces

Let me briefly direct your attention to three interesting facts:

  1. Half of the edges are gone. This is because information now flows in only one direction.
  2. Every node is reachable; no node has been stranded by the edge pruning.
  3. (C,D) and (D,C) are necessarily transient states; only (C, C) and (D,D) can recur indefinitely.

Intertemporal Retaliation

Four qualities of successful IPD strategies are: nice, forgiving, non-envious, and retaliating. How does retaliation work in the “normal” IPD?

ISD - Traditional IPD retaliation

Here we have two cases of retaliation:

  1. At the first time-step, Player A defects “unfairly”. Incensed, Player B retaliates (defects) next turn.
  2. At the fourth time-step, Player B takes advantage of A’s goodwill. Outraged, Player A punishes B next turn.

Note the easy two-way symmetry. But in the ISD case, the question of retaliation becomes very complex:

  1. Present-selves may “punish” future-selves by taking an earlier reward, now.
  2. But future-selves cannot punish present-selves, obviously, because time does not flow in that direction.

What, then, is to motivate our present-selves to “keep the faith”?  To answer this, we need only appeal to the feedback nature of personal rules (explored last time)!

I’ll let Ainslie explain:

As Bratman has correctly argued (Bratman 1999, pp. 35-57), a present “person-stage” can’t retaliate against the defection of a prior one, a difference that disqualifies the prisoner’s dilemma in its classical form as a rationale for consistency. However, insofar as a failure to cooperate will induce future failures, a current decision-maker contemplating defection faces a danger of the same kind as retaliation…

With the question of retaliation repaired, the analogy between IPD and ISD seems secure. Ainslie has earned the right to invoke IPD explananda; for example:

The rules of this market are the internal equivalent of “self-enforcing contracts” made by traders who will be dealing with each other repeatedly, contracts that let them do business on the strength of handshakes (Klein & Leffler 1981; Macaulay 1963).

Survival Of The Salient

After casting warfare of successive selves into game theoretic terms, we are in a position to import other concepts. Consider the Schelling point, the notion that salient choices function as an attractor between competitors. Here’s an example of the Schelling point:

Consider a simple example: two people unable to communicate with each other are each shown a panel of four squares and asked to select one; if and only if they both select the same one, they will each receive a prize.Three of the squares are blue and one is red. Assuming they each know nothing about the other player, but that they each do want to win the prize, then they will, reasonably, both choose the red square. Of course, thered square is not in a sense a better square; they could win by both choosing any square. And it is only the “right” square to select if a player can be sure that the other player has selected it; but by hypothesis neither can. However, it is the most salient and notable square, so—lacking any other one—most people will choose it, and this will in fact (often) work.

By virtue of the feedback mechanism discussed above, rules are adapt over time via a kind of variation on natural selection (“survival of the salient“):

Intertemporal cooperation is most threatened by rationalizations that permit exceptions for the choice at hand, and is most stabilized by finding bright lines to serve as criteria for what constitutes cooperation. A personal rule never to drink alcohol, for instance, is more stable than a rule to have only two drinks a day, because the line between some drinking and no drinking is unique (bright), while the two-drinks rule does not stand out from some other number, or define the size of the drinks, and is thus susceptible to reformulation. However, skill at intertemporal bargaining will let you attain more flexibility by using lines that are less bright. This skill is apt to be a key component of the control processes that get called ego functions.

In the vocabulary of our model, it is the peculiarities of the preference bundling module whereby Schelling points are more effectual.

Let us close by, in passing, noting that this line of argument can be generalized into a justification for slippery slope arguments.

Takeaways

  • Warfare of successive selves can be understood in terms of the Prisoner’s Dilemma, where cooperation with oneself is selecting LL, and defection is SS.
  • In fact, intertemporal bargaining can be successfully explained via a modified form of the Iterated Prisoner’s Dilemma, since retaliation works via a unique feedback mechanism.
  • Because our model of willpower spans both a game-theoretic and cognitive grammar, we can make sense of a “survival of the salient” effect, whereby memorable rules persist longer.